题目内容
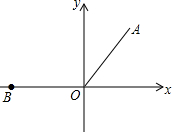 (2012•建宁县质检)如图:在直角坐标系中,线段OA=6cm,OA与y轴的夹角为30°.将线段OA绕原点按逆时针方向旋转到x轴的负半轴上,得到线段OB.
(2012•建宁县质检)如图:在直角坐标系中,线段OA=6cm,OA与y轴的夹角为30°.将线段OA绕原点按逆时针方向旋转到x轴的负半轴上,得到线段OB.(1)点A经过的路径是一条
弧
弧
(填“线段”或“弧”),并求出此“路径”的长度;(2)求线段OA转到OB位置时,OA所“扫描”过的图形的面积.
分析:(1)由于线段OA绕原点按逆时针方向旋转到x轴的负半轴上的OB的位置,根据旋转的性质得到点A到O点的距离不变,为6cm,则点A经过的路径是一条以O为圆心,6cm为半径的一段弧;然后根据弧长公式计算此段路径;
(2)直接根据扇形的面积公式计算即可.
(2)直接根据扇形的面积公式计算即可.
解答:解:(1)填“弧”;
∵∠AOB=90°+30°=120°,OA=6,
∴弧AB的长=
=4π,
即点A经过的路径长为4πcm;
(2)线段OA转到OB位置时,OA所“扫描”过的图形是一个扇形,其面积=
=12π(cm2).
∵∠AOB=90°+30°=120°,OA=6,
∴弧AB的长=
| 120•π•6 |
| 180 |
即点A经过的路径长为4πcm;
(2)线段OA转到OB位置时,OA所“扫描”过的图形是一个扇形,其面积=
| 120•π•62 |
| 360 |
点评:本题考查了旋转的性质:旋转前后两图形全等;对应点与旋转中心的连线段的夹角等于旋转角;对应点到旋转中心的距离相等.也考查了弧长公式和扇形的面积公式.

练习册系列答案
相关题目

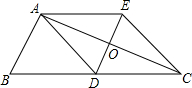 (2012•建宁县质检)如图:△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB与AC、AE分别交于点O、E,连接EC.
(2012•建宁县质检)如图:△ABC中,AD是边BC上的中线,过点A作AE∥BC,过点D作DE∥AB与AC、AE分别交于点O、E,连接EC.