Question

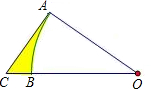如图，OAB是半径为6、圆心角∠AOB=30°的扇形，AC切弧AB于点A交半径OB的延长线于点C，则图中阴影部分的面积为

 

（答案保留π）．

Answer 1

分析：由AC切弧AB于点A，得到∠OAC=90°，再由∠AOB=30°，OA=6，得到AC=

3

3

OA=

3

3

×6=2

3

，而S_阴影部分=S_△OAC-S_扇形OAB，
然后根据扇形和三角形的面积公式计算即可．

解答：解：∵AC切弧AB于点A，
∴∠OAC=90°，
而∠AOB=30°，OA=6，
∴AC=

3

3

OA=

3

3

×6=2

3

，
∴S_阴影部分=S_△OAC-S_扇形OAB=

1

2

×6×2

3

-

30π×62

360

=6

3

-3π．
故答案为：6

3

-3π．

点评：本题考查了扇形的面积公式：S=

nπR2

360

，其中n为扇形的圆心角的度数，R为圆的半径），或S=

1

2

lR，l为扇形的弧长，R为半径．同时考查了切线的性质和含30度的直角三角形三边的关系．