Question

育新中学校园内有一块直角三角形（Rt△ABC）空地，如图所示，园艺师傅以角平分线AD为界，在其两侧分别种上了不同的花草，在△ABD区域内种植了一串红，在△ACD区域内种植了鸡冠花，并量得两直角边AB=20m，AC=10m，求一串红与鸡冠花两种花草各种植的面积（提示：利用角平分线的性质）

Answer 1

分析：过点D作DE⊥AB于E，过点D作DF⊥AC于F，根据角平分线上的点到角的两边的距离相等可得DE=DF，再根据△ABC的面积求出DE，然后利用三角形的面积公式列式进行计算即可得解．

解答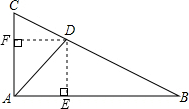：解：如图，过点D作DE⊥AB于E，过点D作DF⊥AC于F，
∵AD是∠BAC的平分线，
∴DE=DF，
∵AB=20m，AC=10m，
∴S_△ABC=

1

2

×20×10=

1

2

×20•DE+

1

2

×10•DF，
解得DE=

20

3

，
∴△ACD的面积=

1

2

×10×

20

3

=

100

3

m²，
△ABD的面积=

1

2

×20×

20

3

=

200

3

m²．

点评：本题考查了角平分线上的点到角的两边的距离相等的性质，三角形的面积，作辅助线，利用三角形的面积求出DE的长度的是解题的关键．