题目内容
【题目】已知二次函数y=﹣x2+2x+m的部分图象如图所示,则关于x的一元二次方程﹣x2+2x+m=0的解为 . 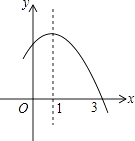
【答案】x1=﹣1或x2=3
【解析】解:依题意得二次函数y=﹣x2+2x+m的对称轴为x=1,与x轴的一个交点为(3,0),
∴抛物线与x轴的另一个交点横坐标为1﹣(3﹣1)=﹣1,
∴交点坐标为(﹣1,0)
∴当x=﹣1或x=3时,函数值y=0,
即﹣x2+2x+m=0,
∴关于x的一元二次方程﹣x2+2x+m=0的解为x1=﹣1或x2=3.
所以答案是:x1=﹣1或x2=3.
【考点精析】掌握抛物线与坐标轴的交点是解答本题的根本,需要知道一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】已知该公司每天能精加工蔬菜6吨或粗加工蔬菜16吨(两种加工不能同时进行),某蔬菜公司收购蔬菜进行销售的获利情况如下表所示:
销售方式 | 直接销售 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 100 | 250 | 450 |
(1)现在该公司收购了140吨蔬菜,如果要求在18天内全部销售完这140吨蔬菜,请完成下列表格:
销售方式 | 全部直接销售 | 全部粗加工后销售 | 尽量精加工,剩余部分直接销售 |
获利(元) |
(2)如果先进行精加工,然后进行粗加工,要求15天刚好加工完140吨蔬菜,则应如何分配加工时间?