题目内容
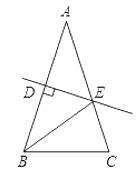
【题目】在等边△ABC中,AO是高,D为AO上一点,以CD为一边,在CD下方作等边△CDE,连接BE.
(1)求证:AD=BE;
(2)过点C作CH⊥BE,交BE的延长线于H,若BC=8,求CH的长.
【答案】
(1)证明:∵△ABC和△CDE都是等边三角形,
∴CA=CB,CD=CE,∠ACB=60°,∠DCE=60°,
∴∠ACD+∠BCD=∠ACB=60°,∠BCE+∠BCD=∠DCE=60°,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
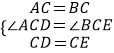 ,
,
∴△ACD≌△BCE(SAS);
∴AD=BE
(2)解:∵△ABC是等边三角形,AO是BC边上的高,
∴∠BAC=60°,且AO平分∠BAC,
∴∠CAD= ![]() ∠BAC=
∠BAC= ![]() ×60°=30°.
×60°=30°.
∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∴∠CBE=30°.
又∵CH⊥BE,BC=8,
∴在Rt△BCH中,CH= ![]() BC=
BC= ![]() ×8=4,即CH=4
×8=4,即CH=4
【解析】(1)根据等边三角形的性质得出CA=CB,CD=CE,∠ACB=60°,∠DCE=60°,从而得出∠ACD=∠BCE.然后利用SAS判断出△ACD≌△BCE ,根据全等三角形的性质得出AD=BE ;
(2)根据等腰三角形,底边上的三线合一得出∠CAD=30°.根据△ACD≌△BCE,得出∠CAD=∠CBE,从而得出∠CBE=30°.然后根据含30![]() 角的直角三角形的边角关系得出CH的长度。
角的直角三角形的边角关系得出CH的长度。

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目