题目内容
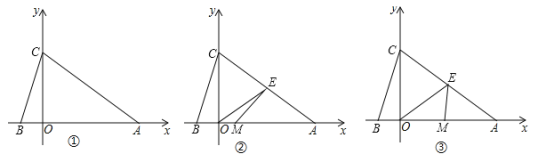
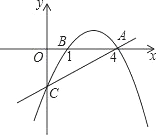
【题目】如图,抛物线y1=﹣![]() x2+bx+c经过点A(4,0)和B(1,0),与y轴交于点C.
x2+bx+c经过点A(4,0)和B(1,0),与y轴交于点C.
(1)求出抛物线的解析式;
(2)求点C的坐标及抛物线的顶点坐标;
(3)设直线AC的解析式为y2=mx+n,请直接写出当y1<y2时,x的取值范围.
【答案】(1)抛物线的解析式是y=﹣![]() x2+
x2+![]() x﹣2;(2)顶点坐标是(
x﹣2;(2)顶点坐标是(![]() ,
,![]() );(3) x<0或x>4.
);(3) x<0或x>4.
【解析】
(1)代入A和B点并联立方程求解即可;
(2)令x=0求解c点坐标,再运用配方法将一般式化为顶点式即可;
(3)由图像可知,C点左侧以及A点右侧部分均符合问题要求.
(1)根据题意得: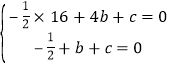 ,解得
,解得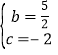
则抛物线的解析式是y=﹣![]() x2+
x2+![]() x﹣2;
x﹣2;
(2)在y=![]() x2+
x2+![]() x﹣2中令x=0,则y=﹣2,则C的坐标是(0,﹣2).
x﹣2中令x=0,则y=﹣2,则C的坐标是(0,﹣2).
y=﹣![]() x2+
x2+![]() x﹣2=﹣
x﹣2=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,则抛物线的顶点坐标是(
,则抛物线的顶点坐标是(![]() ,
,![]() );
);
(3) 由图像可知,C点左侧以及A点右侧部分均符合问题要求,故当x<0或x>4时均满足y1<y2.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了让“两会”精神深入青年学生,增强学子们的历史使命和社会责任感,某高校党委举办了“奋力奔跑同心追梦”两会主题知识竞答活动,文学社团为选派优秀同学参加学校竞答活动,提前对甲、乙两位同学进行了6次测验:
①收集数据:分别记录甲、乙两位同学6次测验成绩(单位:分)
甲 | 82 | 78 | 82 | 83 | 86 | 93 |
乙 | 83 | 81 | 84 | 86 | 83 | 87 |
②整理数据:列表格整理两位同学的测验成绩(单位:分)
1 | 2 | 3 | 4 | 5 | 6 | |
甲 | 82 | 78 | 82 | 83 | 86 | 93 |
乙 | 83 | 81 | 84 | 86 | 83 | 87 |
③描述数据:根据甲、乙两位同学的成绩绘制折线统计图

④分析数据:两组成绩的平均数、中位数、众数、方差如下表:
同学 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 84 | 82.5 | __________ | 16.3 |
乙 | 84 | 83.5 | 83 | __________ |
得出结论:结合上述统计过程,回答下列问题:
(1)补全④中表格;
(2)甲、乙两名同学中,_______(填甲或乙)的成绩更稳定,理由是______________________
(3)如果由你来选择一名同学参加学校的竞答活动,你会选择__________(填甲或乙),理由是___________