题目内容
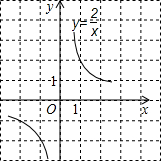 函数y=
函数y=| 2 |
| x |
| 2 |
| x |
分析:求直线平移后的解析式时要注意平移时k的值不变,只有b发生变化.上下平移时只需让b的值加减即可.
解答:解:y=-x+1的k=-1,b=1,向上平移2个单位后,新直线的k=-1,b=1+2=3.
∴新直线的解析式为:y=-x+3.
有交点,则
,
解得
或
.
那么所得直线与函数y=
的图象的交点共有2个.
故答案为:2.
∴新直线的解析式为:y=-x+3.
有交点,则
|
解得
|
|
那么所得直线与函数y=
| 2 |
| x |
故答案为:2.
点评:本题考查了一次函数的平移变换及与反比例函数的交点问题,同学们要重点掌握.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 若反比例函数y=
若反比例函数y=| -2 |
| x |
| A、S1=S2 |
| B、S1>S2 |
| C、S1<S2 |
| D、无法判断 |
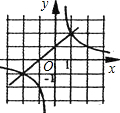 一次函数y=kx+b与反比例函数y=
一次函数y=kx+b与反比例函数y= 已知反比例函数y=
已知反比例函数y=