Question

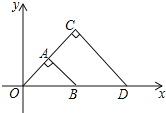
【题目】如图，△OAB与△OCD是以点O为位似中心的位似图形，相似比为1：2，∠OCD=90°，CO=CD．若B（2，0），则点C的坐标为（ ）

A．（2，2） B．（1，2） C．（，2） D．（2，1）

Answer 1

【答案】A

【解析】

试题分析：首先利用等腰直角三角形的性质得出A点坐标，再利用位似是特殊的相似，若两个图形△ABC和△A′B′C′以原点为位似中心，相似比是k，△ABC上一点的坐标是（x，y），则在△A′B′C′中，它的对应点的坐标是（kx，ky）或（﹣kx，ky），进而求出即可．

解：∵∠OAB=∠OCD=90°，CO=CD，Rt△OAB与Rt△OCD是位似图形，点B的坐标为（2，0），

∴BO=2，则AO=AB=，

∴A（1，1），

∵等腰Rt△OAB与等腰Rt△OCD是位似图形，O为位似中心，相似比为1：2，

∴点C的坐标为：（2，2）．

故选：A．