题目内容
已知关于x的方程(n-1)x2+mx+1=0①有两个相等的实数根.
(1)用含n的代数式表示m2;
(2)求证:关于x的m2x2-2mx-m2-2n2+3=0方程②必有两个不相等的实数根;
(3)若方程①的一根的相反数恰好是方程②的一个根,求代数式m2n+12n的值.
解:(1)∵关于x的方程(n-1)x2+mx+1=0①有两个相等的实数根,
∴△1=b2-4ac=m2-4(n-1)×1=0,且n-1≠0,
解得,m2=4(n-1)(n≠1);
∵m2≥0,n≠1.
∴m2=4(n-1),且n>1.
(2)证明:由(1)知,m2=4(n-1)(n>1),即m≠0.
∵关于x的m2x2-2mx-m2-2n2+3=0方程的二次项系数a=m2,一次项系数b=-2m,常数项c=-m2-2n2+3,
∴△2=b2-4ac
=(-2m)2-4m2•(-m2-2n2+3)
=4m2•(m2+2n2-2)
=4m2•[4(n-1)+2n2-2]
=8m2(n+3)(n-1).
∵m2>0,n>1.
∴△2>0,
∴方程②有两个不相等的实数根;
(3)解:由m2=4(n-1),得n-1=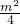 .代入第一个方程,得
.代入第一个方程,得
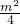 x2+mx+1=0,解得x=-
x2+mx+1=0,解得x=- .
.
把 代入第二个方程,得
代入第二个方程,得
m2×( )2-2m×(
)2-2m×( )-m2-2n2+3=0.
)-m2-2n2+3=0.
整理得2n2+4n=7.
∴m2n十12n=n(m2+12)
=n(4n-4+12)
=4n2+8n
=2(2n2+4n)
=14.
分析:(1)、(2)方程①有两个相等的实数根,则n-1≠0,△1=0,可得m2=4n-4>0,代入方程②的判别式△2=8m2(n+3)(n-1)>0.
(3)把(1)中根据①有两个相等的实数根,即方程的判别式△1=0,得到的关于m,n的一个等式,变形为用含m的代数式表示n的形式,消去方程①中的m,然后解方程①,求出方程的根,根据若方程①的一根的相反数恰好是方程②的一个根,即可求解.
点评:本题考查了根的判别式、根与系数的关系.一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
∴△1=b2-4ac=m2-4(n-1)×1=0,且n-1≠0,
解得,m2=4(n-1)(n≠1);
∵m2≥0,n≠1.
∴m2=4(n-1),且n>1.
(2)证明:由(1)知,m2=4(n-1)(n>1),即m≠0.
∵关于x的m2x2-2mx-m2-2n2+3=0方程的二次项系数a=m2,一次项系数b=-2m,常数项c=-m2-2n2+3,
∴△2=b2-4ac
=(-2m)2-4m2•(-m2-2n2+3)
=4m2•(m2+2n2-2)
=4m2•[4(n-1)+2n2-2]
=8m2(n+3)(n-1).
∵m2>0,n>1.
∴△2>0,
∴方程②有两个不相等的实数根;
(3)解:由m2=4(n-1),得n-1=
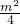 .代入第一个方程,得
.代入第一个方程,得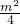 x2+mx+1=0,解得x=-
x2+mx+1=0,解得x=- .
.把
 代入第二个方程,得
代入第二个方程,得m2×(
 )2-2m×(
)2-2m×( )-m2-2n2+3=0.
)-m2-2n2+3=0.整理得2n2+4n=7.
∴m2n十12n=n(m2+12)
=n(4n-4+12)
=4n2+8n
=2(2n2+4n)
=14.
分析:(1)、(2)方程①有两个相等的实数根,则n-1≠0,△1=0,可得m2=4n-4>0,代入方程②的判别式△2=8m2(n+3)(n-1)>0.
(3)把(1)中根据①有两个相等的实数根,即方程的判别式△1=0,得到的关于m,n的一个等式,变形为用含m的代数式表示n的形式,消去方程①中的m,然后解方程①,求出方程的根,根据若方程①的一根的相反数恰好是方程②的一个根,即可求解.
点评:本题考查了根的判别式、根与系数的关系.一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目