题目内容
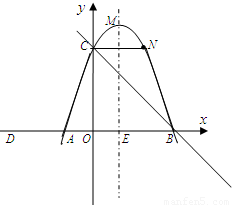
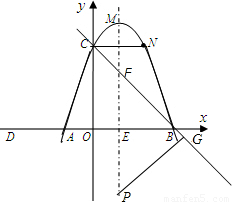
如图,已知等腰梯形ABNC的边AB在x轴上,点C在y轴的正方向上,C(0,6),N (4,6),且AC=
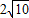 .
.(1)求点A的坐标;
(2)若二次函数y=ax2+bx+c的图象经过A、C、B三点,求二次函数的解析式,并写出顶点M的坐标;
(3)点P是这个二次函数的对称轴上一动点,请探索:是否存在这样的点P,使P点到直线BC与x轴的距离相等?如果存在,请求出点P的坐标;如果不存在,请说明理由.
【答案】分析:(1)在△AOC中,运用勾股定理求OA即可;
(2)根据梯形,抛物线的对称性求B点坐标,再设抛物线的交点式,把C点坐标代入求抛物线解析式,将解析式配方求顶点M坐标;
(3)设直线BC与抛物线对称轴交于F点,直线BC与x轴夹角为45°,则P点到直线BC=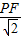 ,根据题意列方程求P点坐标.
,根据题意列方程求P点坐标.
解答:解:(1)在Rt△AOC中,∵AC= ,OC=6,∴AO=2,∴A(-2,0);
,OC=6,∴AO=2,∴A(-2,0);
(2)由等腰梯形的对称性可知OB=CN+OA=4+2=6,即B(6,0),
设抛物线解析式为y=a(x+2)(x-6),将C(0,6)代入,得a=- ,
,
∴y=- (x+2)(x-6),即y=-
(x+2)(x-6),即y=- x2+2x+6=-
x2+2x+6=- (x-2)2+8,顶点M(2,8);
(x-2)2+8,顶点M(2,8);
(3)存在.
如图,设直线BC与抛物线对称轴交于F点,直线BC解析式为y=-x+6,与x轴夹角为45°,F(2,4),
设P(2,m)则PF=|4-m|,
由等腰直角三角形的性质可知,P点到直线BC=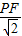 ,
,
依题意,得|m|=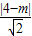 ,解得m=4
,解得m=4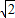 -4或-4
-4或-4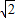 -4.
-4.
点评:本题考查了二次函数的综合运用.关键是根据题意求A点坐标及抛物线解析式,判断△OBC为等腰直角三角形,利用特殊三角形的性质求解.
(2)根据梯形,抛物线的对称性求B点坐标,再设抛物线的交点式,把C点坐标代入求抛物线解析式,将解析式配方求顶点M坐标;
(3)设直线BC与抛物线对称轴交于F点,直线BC与x轴夹角为45°,则P点到直线BC=
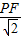 ,根据题意列方程求P点坐标.
,根据题意列方程求P点坐标.解答:解:(1)在Rt△AOC中,∵AC=
 ,OC=6,∴AO=2,∴A(-2,0);
,OC=6,∴AO=2,∴A(-2,0);(2)由等腰梯形的对称性可知OB=CN+OA=4+2=6,即B(6,0),
设抛物线解析式为y=a(x+2)(x-6),将C(0,6)代入,得a=-
 ,
,∴y=-
 (x+2)(x-6),即y=-
(x+2)(x-6),即y=- x2+2x+6=-
x2+2x+6=- (x-2)2+8,顶点M(2,8);
(x-2)2+8,顶点M(2,8);(3)存在.
如图,设直线BC与抛物线对称轴交于F点,直线BC解析式为y=-x+6,与x轴夹角为45°,F(2,4),
设P(2,m)则PF=|4-m|,
由等腰直角三角形的性质可知,P点到直线BC=
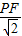 ,
,依题意,得|m|=
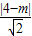 ,解得m=4
,解得m=4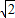 -4或-4
-4或-4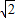 -4.
-4.
点评:本题考查了二次函数的综合运用.关键是根据题意求A点坐标及抛物线解析式,判断△OBC为等腰直角三角形,利用特殊三角形的性质求解.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案
相关题目
 ,
, 3、如图,已知等腰梯形ABCD中,AD∥BC,∠B=60°,AD=2,BC=8,则此等腰梯形的周长为( )
3、如图,已知等腰梯形ABCD中,AD∥BC,∠B=60°,AD=2,BC=8,则此等腰梯形的周长为( ) 如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC=
如图,已知等腰梯形ABCD中,AD∥BC,BD⊥DC,∠DBC= 13、如图,已知等腰梯形ABCD,AD∥BC,AD=5cm,BC=11cm,高DE=4cm,则梯形的周长为
13、如图,已知等腰梯形ABCD,AD∥BC,AD=5cm,BC=11cm,高DE=4cm,则梯形的周长为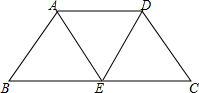 如图,已知等腰梯形ABCD是由三个边长为2的全等的正三角形围成的,则等腰梯形ABCD的面积是
如图,已知等腰梯形ABCD是由三个边长为2的全等的正三角形围成的,则等腰梯形ABCD的面积是