题目内容
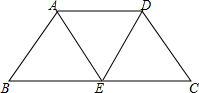如图，已知等腰梯形ABCD是由三个边长为2的全等的正三角形围成的，则等腰梯形ABCD的面积是3
| 3 |
3
．| 3 |
分析：利用等边三角形的性质得出AF的长，进而利用梯形面积公式求出即可．
解答：
解：过点A作AF⊥BE于点F，
∵等腰梯形ABCD是由三个边长为2的全等的正三角形围成的，
∴∠B=60°，BF=BE=1，AB=2，
∴AF=
，
∴等腰梯形ABCD的面积是：
×（2+2+2）×
=3
．
故答案为：3
．
解：过点A作AF⊥BE于点F，∵等腰梯形ABCD是由三个边长为2的全等的正三角形围成的，
∴∠B=60°，BF=BE=1，AB=2，
∴AF=
| 3 |
∴等腰梯形ABCD的面积是：
| 1 |
| 2 |
| 3 |
| 3 |
故答案为：3
| 3 |
点评：此题主要考查了等边三角形的性质以及勾股定理和梯形面积公式等知识，根据已知得出梯形的高是解题关键．
练习册系列答案
培优好卷单元加期末卷系列答案
一线名师权威作业本系列答案
相关题目
，
3、如图，已知等腰梯形ABCD中，AD∥BC，∠B=60°，AD=2，BC=8，则此等腰梯形的周长为（ ）
如图，已知等腰梯形ABCD中，AD∥BC，BD⊥DC，∠DBC=
13、如图，已知等腰梯形ABCD，AD∥BC，AD=5cm，BC=11cm，高DE=4cm，则梯形的周长为