��Ŀ����
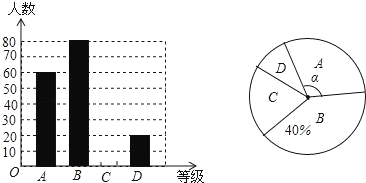
����Ŀ������ʵ����ѧ����ҵ��������������ҵ�ĸ��һ����Ҫ�ٴ룮ij��ѧΪ�˽ⱾУѧ��ƽ��ÿ��Ŀ�����ҵʱ�䣬�����ȡ����ѧ�������ʾ����飬������������ΪA��B��C��D�ĸ��ȼ���A��1Сʱ���ڣ�B��1Сʱ--1.5Сʱ��C��1.5Сʱ--2Сʱ��D��2Сʱ���ϣ����ݵ�������������ͼ��ʾ�����ֲ�������ͳ��ͼ�������ͼ����Ϣ����������⣺
��1����У�������� ѧ����
��2���뽫����ͳ��ͼ����������
��3����ʾ�ȼ�A������Բ�ĽǦ��Ķ����� ��
��4���ڴ˴ε����ʾ��У��ס����������2��ƽ��ÿ�������ҵ������2Сʱ���ϣ�����4������ѡ2��ȥ�μ���̸�����б�������״ͼ�ķ�����ѡ����2�����Բ�ͬ�༶�ĸ��ʣ�
���𰸡���1��200����2����ͼ����������3��108������4��![]() .
.
��������
�����������1������B�����������ռ�İٷֱȼ������������
��2�����C�������Ӷ���ȫͳ��ͼ��
��3����A�����������������ٳ���360�㣬���ɵõ�Բ�ĽǦ��Ķ�����
��4������װ�ѧ��ΪA1��A2���Ұ�ѧ��ΪB1��B2���������⻭������ͼ���ٸ��ݸ��ʹ�ʽ��ʽ���㼴�ɣ�
�����������1�����������ѧ�����ǣ�80��40%=200���ˣ���
�ʴ�Ϊ��200��
��2��C��������ǣ�200-60-80-20=40���ˣ���
��ͼ���£�
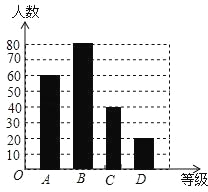
��3����������ã���=![]() ��360��=108�㣬
��360��=108�㣬
�ʴ�Ϊ��108�㣻
��4����װ�ѧ��ΪA1��A2���Ұ�ѧ��ΪB1��B2��
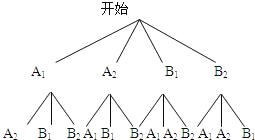
һ����12�ֵȿ��ܽ��������2�����Բ�ͬ�༶����8�֣�
��P��2�����Բ�ͬ�༶��=![]() ��
��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
