题目内容
如图1,在一直角边长为4米的等腰直角三角形地块的每一个正方形网格的格点(纵横直线的交点及三角形顶点) 上都种植同种农作物,根据以往种植实验发现,每株农作物的产量y(单位:千克) 受到与它周围直线距离不超过1米的同种农作物的株数x(单位:株) 的影响情况统计如下表:
(1)通过观察上表,猜测y与x之间之间存在哪种函数关系,求出函数关系式并加以验证;
(2)根据种植示意图填写下表,并求出这块地平均每平方米的产量为多少千克?
(3)有人为提高总产量,将上述地块拓展为斜边长为6米的等腰直角三角形,采用如图2所示的方式,在每个正方形网格的格点上都种植了与前面相同的农作物,共种植了16株,请你通过计算平均每平方米的产量,来比较那种种植方式更合理?

| x(株) | 1 | 2 | 3 | 4 |
| y(千克) | 21 | 18 | 15 | 12 |
(2)根据种植示意图填写下表,并求出这块地平均每平方米的产量为多少千克?
| y(千克) | 21 | 18 | 15 | 12 |
| 频数 | | | | |

(1)y=﹣3x+24
当x=3时 y=﹣3×3+24=15;当x=4时 y=﹣3×4+24=12。
∴y=﹣3x+24是符合条件的函数关系。
(2)填表如下:
30(千克 )
(3)按图(1)的种植方式更合理。
当x=3时 y=﹣3×3+24=15;当x=4时 y=﹣3×4+24=12。
∴y=﹣3x+24是符合条件的函数关系。
(2)填表如下:
| y(千克) | 21 | 18 | 15 | 12 |
| 频数 | 2 | 4 | 6 | 3 |
(3)按图(1)的种植方式更合理。
分析:(1)设y=kx+b,然后根据表格数据,取两组数x=1,y=21和x=2,y=18,利用待定系数法求一次函数解析式解答。
(2)根据图1查出与它周围距离为1米的农作物分别是1株、2株、3株、4株棵树即为相应的频数,然后利用加权平均数的计算方法列式进行计算即可得解。
(3)先求出图2的面积,根据图形查出与它周围距离为1米的农作物分别是1株、2株、3株、4株棵树即为相应的频数,然后利用加权平均数的计算方法列式进行计算求出平均每平方米的产量,然后与(2)的计算进行比较即可得解。
解(1)观察表示内容,每株农作物的产量y随与它周围直线距离不超过1米的同种农作物的株数x的增加而减少3,可知二者之间是一次函数关系,设y=kx+b,
把x=1,y=21和x=2,y=18代入y=kx+b得,
 ,解得
,解得 。则y=﹣3x+24。
。则y=﹣3x+24。当x=3时 y=﹣3×3+24=15;当x=4时 y=﹣3×4+24=12。
∴y=﹣3x+24是符合条件的函数关系。
(2)填表如下:
| y(千克) | 21 | 18 | 15 | 12 |
| 频数 | 2 | 4 | 6 | 3 |
 ×4×4=8(m2),
×4×4=8(m2),∴平均每平方米的产量为:(21×2+18×4+15×6+12×3)÷8=30(千克 )。
(3)∵图2地块的面积:
 ×6×3=9(m2),
×6×3=9(m2),y(千克)21、18、15、12的频数分别为3、4、5、4,
∴图2地块平均每平方米产量:(21×3+18×4+15×5+12×4)÷9=258÷9≈28.67(千克)。
∵30>28.67,
∴按图(1)的种植方式更合理。

练习册系列答案
相关题目



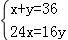
 的解是 ( )
的解是 ( )



 ,则代数式
,则代数式 的值为__ _____。
的值为__ _____。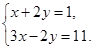
 时,由于粗心,甲看错了方程组中的a,而得到解为
时,由于粗心,甲看错了方程组中的a,而得到解为 ;乙看错了方程组中的b而得到解为
;乙看错了方程组中的b而得到解为 。
。