题目内容
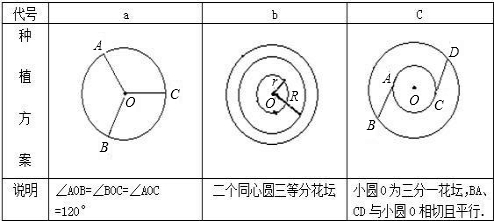
在一次上数学实践活动课时,老师布置了如下活动内容:“学校准备在校园内的一块空地上建一个半径为6米的圆形花坛,为便于管理和美观,打算种上三种颜色的花,相同颜色的花集中种植,且所占的面积相同、整个花坛成轴对称图形或中心对称图形,要求全班每个同学设计一个符合要求的种植方案(图案)”.下面是三位同学设计的种植方案(图案):

(1)请问以上三个图案中是轴对称图形的有______.是中心对称图形的有______.(分别填上图案的代号);
(2)求出图b或c中的r、R、AB的长(结果可保留根号),并由此推断、证明:当花坛半径为a(a>0)时,a、r、R三者之间的数量关系;
(3)如果你也是此次活动的参与者,请你设计二个种植方案(图案) (要求不能与上面图案重复,画图工具不限,不写作法和证明,但要简要说明).
【答案】分析:(1)根据轴对称的定义和中心对称的定义作答即可;
(2)b中,根据小圆或圆环的面积为12π作答即可;c中,利用相切构成直角三角形可求得AB长;根据三部分之间的面积关系可得到关系式;
(3)方案不唯一,可在所给3种方案的基础上进行改造.
解答:解:(1)根据中心对称图形及轴对称图形的定义可得答案为a、b;b、c;
(2)根据题意得:在图b中,r2π=12π,r=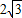 (米)
(米)
R2π=24π,
R=2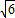 (米),
(米),
在图c中,BA切小⊙O于A,OA⊥AB
故在直角△ABO中,AB=CD=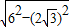 =
=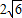 (米)
(米)
a与r、R之间的数量关系是:a2=r2+R2
证明:∵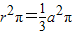 ,
,
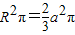 ,
,
∴r2π+R2π=a2π
∴a2=r2+R2
(3)如图所示:
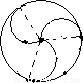 或
或 或
或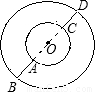 .
.
点评:考查了中心对称图形和轴对称图形的定义及有关相等面积的计算;得到每部分的面积是解决本题的突破点.
(2)b中,根据小圆或圆环的面积为12π作答即可;c中,利用相切构成直角三角形可求得AB长;根据三部分之间的面积关系可得到关系式;
(3)方案不唯一,可在所给3种方案的基础上进行改造.
解答:解:(1)根据中心对称图形及轴对称图形的定义可得答案为a、b;b、c;
(2)根据题意得:在图b中,r2π=12π,r=
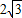 (米)
(米)R2π=24π,
R=2
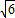 (米),
(米),在图c中,BA切小⊙O于A,OA⊥AB
故在直角△ABO中,AB=CD=
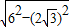 =
=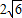 (米)
(米)a与r、R之间的数量关系是:a2=r2+R2
证明:∵
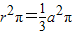 ,
,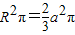 ,
,∴r2π+R2π=a2π
∴a2=r2+R2
(3)如图所示:
 或
或 或
或 .
.点评:考查了中心对称图形和轴对称图形的定义及有关相等面积的计算;得到每部分的面积是解决本题的突破点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在一次课外数学实践活动中,小明站在操场的A处,他的两侧分别是旗杆CD和一幢教学楼EF,点A、D、F在同一直线上,从A处测得旗杆顶部和教学楼顶部的仰角分别为45°和60°,已知DF=14m,EF=15m,求旗杆CD高.(结果精确到0.1m,参考数据:
如图,在一次课外数学实践活动中,小明站在操场的A处,他的两侧分别是旗杆CD和一幢教学楼EF,点A、D、F在同一直线上,从A处测得旗杆顶部和教学楼顶部的仰角分别为45°和60°,已知DF=14m,EF=15m,求旗杆CD高.(结果精确到0.1m,参考数据: 如图,在一次课外数学实践活动中,小明站在操场的A处,他的两侧分别是旗杆CD和一幢教学楼EF,点A、D、F在同一直线上,从A处测得旗杆顶部和教学楼顶部的仰角分别为45°和60°,已知DF=14m,EF=15m,求旗杆CD高.(结果精确到0.1m,参考数据:
如图,在一次课外数学实践活动中,小明站在操场的A处,他的两侧分别是旗杆CD和一幢教学楼EF,点A、D、F在同一直线上,从A处测得旗杆顶部和教学楼顶部的仰角分别为45°和60°,已知DF=14m,EF=15m,求旗杆CD高.(结果精确到0.1m,参考数据: ≈1.41,
≈1.41, ≈1.73)
≈1.73)
