题目内容
如图，在一次课外数学实践活动中，小明站在操场的A处，他的两侧分别是旗杆CD和一幢教学楼EF，点A、D、F在同一直线上，从A处测得旗杆顶部和教学楼顶部的仰角分别为45°和60°，已知DF=14m，EF=15m，求旗杆CD高．（结果精确到0.1m，参考数据：| 2 |
| 3 |
分析：在RT△EFA中，利用三角函数的关系求出AF的长，然后可得出AD的长，继而在RT△ADC中可得出CD的长．
解答：解：在RT△EFA中，cot∠EAF=
=
，
又∵EF=15，
∴AF=5
，
∴AD=DF-FA=14-5
，
在Rt△ADC中，∵CD=AD，
∴CD=14-5
≈5.4（m）
| AF |
| EF |
| ||
| 3 |
又∵EF=15，
∴AF=5
| 3 |
∴AD=DF-FA=14-5
| 3 |
在Rt△ADC中，∵CD=AD，
∴CD=14-5
| 3 |
点评：本题考查解直角三角形的应用，难度一般，解答此类题目要注意将实际问题放在数学模型中解答，另外要注意掌握一些特殊角的三角函数值．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
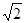≈1.41，
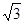≈1.73)
≈1.41，
≈1.73)
≈1.41，
≈1.73)
如图，在一次课外数学实践活动中，小明站在操场的A处，他的两侧分别是旗杆CD和一幢教学楼EF，点A、D、F在同一直线上，从A处测得旗杆顶部和教学楼顶部的仰角分别为45°和60°，已知DF=14m，EF=15m，求旗杆CD高．(结果精确到0.1m，参考数据：
≈1.41，
≈1.73)