题目内容
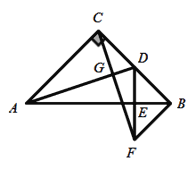
【题目】工人师傅用![]() 米长的铝合金材料制作一个如图所示的矩形窗框,图中的①、②、③区域都是矩形,且
米长的铝合金材料制作一个如图所示的矩形窗框,图中的①、②、③区域都是矩形,且![]() ,
,![]() ,
,![]() 分别是
分别是![]() 、
、![]() 的中点.(说明:图中黑线部分均需要使用铝合金材料制作,铝合金材料宽度忽略不计).
的中点.(说明:图中黑线部分均需要使用铝合金材料制作,铝合金材料宽度忽略不计).

![]() 当矩形窗框
当矩形窗框![]() 的透光面积是
的透光面积是![]() 平方米时,求
平方米时,求![]() 的长度.
的长度.
![]() 当
当![]() 为多长时,矩形窗框
为多长时,矩形窗框![]() 的透光面积最大?最大面积是多少?
的透光面积最大?最大面积是多少?
【答案】(1)![]() (2)当
(2)当![]() 为
为![]() 时,矩形窗框
时,矩形窗框![]() 的透光面积最大,最大面积是
的透光面积最大,最大面积是![]() .
.
【解析】
(1)设AE=x米,根据已知条件表示出BC和AB的长,根据AB×BC=矩形面积2.25列出方程,解方程可得;
(2)先由长×宽=矩形面积得到函数关系式,根据公式可得函数最大值.
(1)∵①、②、③号区域都是矩形,且BE=2AE,设AE=x米,
∴AE=MN=DF=x米,BE=CF=2x米,
∴BC=![]() ,
,
∴![]() 3x=2.25,解得:x1=
3x=2.25,解得:x1=![]() ,x2=
,x2=![]() ,
,
∴AE的长度是![]() 米或
米或![]() 米;
米;
(2)设矩形ABCD的面积是y平方米,
则y=3x![]() =-7x2+8x,
=-7x2+8x,
当x=-![]() =
=![]() 时,y最大=
时,y最大=![]() ×4=
×4=![]() ,
,
答:当AE为![]() 时,矩形窗框ABCD的透光面积最大,最大面积是
时,矩形窗框ABCD的透光面积最大,最大面积是![]() .
.

【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
销售单价(元) | x |
销售量y(件) |
|
销售玩具获得利润w(元) |
|
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?