题目内容
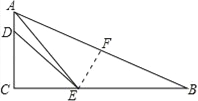
【题目】已知如图,在Rt△ABC中,∠ACB=90°,AE平分∠BAC交BC于点E,D为AC上的点,BE=DE.
(1)求证:∠B+∠EDA=180°;
(2)求![]() 的值.
的值.
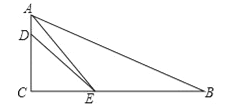
【答案】(1)答案见解析;(2)2.
【解析】试题分析(1)过E作AB的垂线,根据角平分线的性质得出EC=EF,再根据HL得出△ECD≌△EFB,从而得出∠EDC=∠B,再根据∠EDC+∠EDA=180°,即可得出答案;
(2)根据(1)证出的全等得出CD=FB,同理得出Rt△EAC≌Rt△EAF,从而得出CA=FA,再根据![]() ,即可得出答案.
,即可得出答案.
解:(1)过E作AB的垂线,垂足是F,
∵AE是角平分线,∠C=90°
∴EC=EF,
又∵EB=ED,
在Rt△ECD和Rt△EFB中,
∵DE=EB,
EC=EF,,
∴△ECD≌△EFB (HL),
∴∠EDC=∠B,
∵∠EDC+∠EDA=180°,
∴∠B+∠EDA=180°;
(2)∵Rt△ECD≌Rt△EFB,
∴CD=FB,
同理Rt△EAC≌Rt△EAF(HL),
∴CA=FA,
∴![]() .
.
点睛: 此题考查了全等三角形的判定与性质,用到的知识点是全等三角形的判定与性质、角平分线的性质,关键是根据题意作出辅助线,构造直角三角形,熟练运用HL判定三角形全等.

练习册系列答案
相关题目