题目内容
（2013•荆州）如图，已知：如图①，直线y=-
x+
与x轴、y轴分别交于A、B两点，两动点D、E分别从A、B两点同时出发向O点运动（运动到O点停止）；对称轴过点A且顶点为M的抛物线y=a（x-k）2+h（a＜0）始终经过点E，过E作EG∥OA交抛物线于点G，交AB于点F，连结DE、DF、AG、BG．设D、E的运动速度分别是1个单位长度/秒和
个单位长度/秒，运动时间为t秒．
（1）用含t代数式分别表示BF、EF、AF的长；
（2）当t为何值时，四边形ADEF是菱形？判断此时△AFG与△AGB是否相似，并说明理由；
（3）当△ADF是直角三角形，且抛物线的顶点M恰好在BG上时，求抛物线的解析式．
| 3 |
| 3 |
| 3 |
（1）用含t代数式分别表示BF、EF、AF的长；
（2）当t为何值时，四边形ADEF是菱形？判断此时△AFG与△AGB是否相似，并说明理由；
（3）当△ADF是直角三角形，且抛物线的顶点M恰好在BG上时，求抛物线的解析式．
分析：（1）首先求出一次函数y=-
x+
与坐标轴交点A、B的坐标，然后解直角三角形求出BF、EF、AF的长；
（2）由EF∥AD，且EF=AD=t，则四边形ADEF为平行四边形，若?ADEF是菱形，则DE=AD=t．由DE=2OE，列方程求出t的值；
如答图1所示，推出∠BAG=∠GAF，∠ABG=∠AGF=30°，证明△AFG与△AGB相似．
（3）当△ADF是直角三角形时，有两种情形，需要分类讨论：
①若∠ADF=90°，如答图2所示．首先求出此时t的值；其次求出点G的坐标，利用待定系数法求出直线BG的解析式，得到点M的坐标；最后利用顶点式和待定系数法求出抛物线的解析式；
②若∠AFD=90°，如答图3所示．解题思路与①相同．
| 3 |
| 3 |
（2）由EF∥AD，且EF=AD=t，则四边形ADEF为平行四边形，若?ADEF是菱形，则DE=AD=t．由DE=2OE，列方程求出t的值；
如答图1所示，推出∠BAG=∠GAF，∠ABG=∠AGF=30°，证明△AFG与△AGB相似．
（3）当△ADF是直角三角形时，有两种情形，需要分类讨论：
①若∠ADF=90°，如答图2所示．首先求出此时t的值；其次求出点G的坐标，利用待定系数法求出直线BG的解析式，得到点M的坐标；最后利用顶点式和待定系数法求出抛物线的解析式；
②若∠AFD=90°，如答图3所示．解题思路与①相同．
解答：解：（1）在直线解析式y=-
x+
中，令x=0，得y=
；令y=0，得x=1．
∴A（1，0），B（0，
），OA=1，OB=
．
∴tan∠OAB=
，∴∠OAB=60°，
∴AB=2OA=2．
∵EG∥OA，∴∠EFB=∠OAB=60°．
∴EF=
=
=t，BF=2EF=2t，
∴AF=AB-BF=2-2t．
（2）①∵EF∥AD，且EF=AD=t，∴四边形ADEF为平行四边形．
若?ADEF是菱形，则DE=AD=t．
由DE=2OD，即：t=2（1-t），解得t=
．
∴t=
时，四边形ADEF是菱形．
②此时△AFG与△AGB相似．理由如下：
如答图1所示，连接AE，
∵四边形ADEF是菱形，
∴∠DEF=∠DAF=60°，
∴∠AEF=30°．
由抛物线的对称性可知，AG=AE，
∴∠AGF=∠AEF=30°．
在Rt△BEG中，BE=
，EG=2，
∴tan∠EBG=
=
，
∴∠EBG=60°，
∴∠ABG=∠EBG-∠EBF=30°．
在△AFG与△AGB中，∵∠BAG=∠GAF，∠ABG=∠AGF=30°，
∴△AFG∽△AGB．
（3）当△ADF是直角三角形时，
①若∠ADF=90°，如答图2所示：
此时AF=2DA，即2-2t=2t，解得t=
．
∴BE=
t=
，OE=OB-BE=
，
∴E（0，
），G（2，
）．
设直线BG的解析式为y=kx+b，将B（0，
），G（2，
）代入得：
，解得k=-
，b=
，
∴y=-
x+
．
令x=1，得y=
，
∴M（1，
）．
设抛物线解析式为y=a（x-1）2+
，点E（0，
）在抛物线上，
∴
=a+
，解得a=-
．
∴y=-
（x-1）2+
=-
x2+
x+
．
②若∠AFD=90°，如答图3所示：
此时AD=2AF，即：t=2（2-2t），解得：t=
．
∴BE=
t=
，OE=OB-BE=
，
∴E（0，
），G（2，
）．
设直线BG的解析式为y=kx+b，将B（0，
），G（2，
）代入得：
，解得k=-
，b=
，
∴y=-
x+
．
令x=1，得y=
，∴M（1，
）．
设抛物线解析式为y=a（x-1）2+
，点E（0，
）在抛物线上，
∴
=a+
，解得a=-
．
∴y=-
（x-1）2+
=-
x2+
x+
．
综上所述，符合条件的抛物线的解析式为：y=-
x2+
x+
或y=-
x2+
x+
．
| 3 |
| 3 |
| 3 |
∴A（1，0），B（0，
| 3 |
| 3 |
∴tan∠OAB=
| 3 |
∴AB=2OA=2．
∵EG∥OA，∴∠EFB=∠OAB=60°．
∴EF=
| BE |
| tan60° |
| ||
|
∴AF=AB-BF=2-2t．
（2）①∵EF∥AD，且EF=AD=t，∴四边形ADEF为平行四边形．
若?ADEF是菱形，则DE=AD=t．
由DE=2OD，即：t=2（1-t），解得t=
| 2 |
| 3 |
∴t=
| 2 |
| 3 |
②此时△AFG与△AGB相似．理由如下：
如答图1所示，连接AE，
∵四边形ADEF是菱形，
∴∠DEF=∠DAF=60°，
∴∠AEF=30°．
由抛物线的对称性可知，AG=AE，
∴∠AGF=∠AEF=30°．
在Rt△BEG中，BE=
2
| ||
| 3 |
∴tan∠EBG=
| EG |
| BE |
| 3 |
∴∠EBG=60°，
∴∠ABG=∠EBG-∠EBF=30°．
在△AFG与△AGB中，∵∠BAG=∠GAF，∠ABG=∠AGF=30°，
∴△AFG∽△AGB．
（3）当△ADF是直角三角形时，
①若∠ADF=90°，如答图2所示：
此时AF=2DA，即2-2t=2t，解得t=
| 1 |
| 2 |
∴BE=
| 3 |
| ||
| 2 |
| ||
| 2 |
∴E（0，
| ||
| 2 |
| ||
| 2 |
设直线BG的解析式为y=kx+b，将B（0，
| 3 |
| ||
| 2 |
|
| ||
| 4 |
| 3 |
∴y=-
| ||
| 4 |
| 3 |
令x=1，得y=
3
| ||
| 4 |
∴M（1，
3
| ||
| 4 |
设抛物线解析式为y=a（x-1）2+
3
| ||
| 4 |
| ||
| 2 |
∴
| ||
| 2 |
3
| ||
| 4 |
| ||
| 4 |
∴y=-
| ||
| 4 |
3
| ||
| 4 |
| ||
| 4 |
| ||
| 2 |
| ||
| 2 |
②若∠AFD=90°，如答图3所示：
此时AD=2AF，即：t=2（2-2t），解得：t=
| 4 |
| 5 |
∴BE=
| 3 |
4
| ||
| 5 |
| ||
| 5 |
∴E（0，
| ||
| 5 |
| ||
| 5 |
设直线BG的解析式为y=kx+b，将B（0，
| 3 |
| ||
| 5 |
|
2
| ||
| 5 |
| 3 |
∴y=-
2
| ||
| 5 |
| 3 |
令x=1，得y=
3
| ||
| 5 |
3
| ||
| 5 |
设抛物线解析式为y=a（x-1）2+
3
| ||
| 5 |
| ||
| 5 |
∴
| ||
| 5 |
3
| ||
| 5 |
2
| ||
| 5 |
∴y=-
2
| ||
| 5 |
3
| ||
| 5 |
2
| ||
| 5 |
4
| ||
| 5 |
| ||
| 5 |
综上所述，符合条件的抛物线的解析式为：y=-
| ||
| 4 |
| ||
| 2 |
| ||
| 2 |
2
| ||
| 5 |
4
| ||
| 5 |
| ||
| 5 |
点评：本题是中考压轴题，涉及二次函数的图象与性质、一次函数的图象与性质、待定系数法、相似三角形、解直角三角形、菱形等知识点．第（3）问中，有两种情形存在，需要分类讨论，避免漏解．
练习册系列答案
相关题目
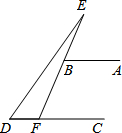（2013•荆州）如图，AB∥CD，∠ABE=60°，∠D=50°，则∠E的度数为（ ）
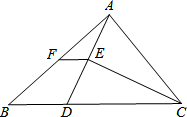（2013•荆州）如图，在△ABC中，BC＞AC，点D在BC上，且DC=AC，∠ACB的平分线CE交AD于E，点F是AB的中点，则S△AEF：S四边形BDEF为（ ）
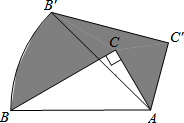（2013•荆州）如图，将含60°角的直角三角板ABC绕顶点A顺时针旋转45°度后得到△AB′C′，点B经过的路径为弧BB′，若∠BAC=60°，AC=1，则图中阴影部分的面积是（ ）
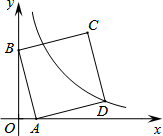（2013•荆州）如图，在平面直角坐标系中，直线y=-3x+3与x轴、y轴分别交于A、B两点，以AB为边在第一象限作正方形ABCD，点D在双曲线
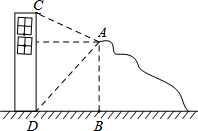（2013•荆州）如图，在高度是21米的小山A处测得建筑物CD顶部C处的仰角为30°，底部D处的俯角为45°，则这个建筑物的高度CD=