题目内容
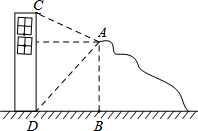（2013•荆州）如图，在高度是21米的小山A处测得建筑物CD顶部C处的仰角为30°，底部D处的俯角为45°，则这个建筑物的高度CD=21+7
| 3 |
21+7
米（结果可保留根号）| 3 |
分析：作AE⊥CD于点E，则△AED和△ABD都是等腰直角三角形，即可求得DE的长，然后在直角三角形中利用三角函数求得CE的长，进而求得CD的长．
解答：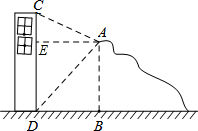
解：作AE⊥CD于点E．
在直角△ABD中，∠ADB=45°，
∴DE=AE=BD=AB=21（米），
在直角△AEC中，CE=AE•tan∠CAE=21×
=7
（米）．
则CD=21+7
．
故答案是：21+7
．
解：作AE⊥CD于点E．在直角△ABD中，∠ADB=45°，
∴DE=AE=BD=AB=21（米），
在直角△AEC中，CE=AE•tan∠CAE=21×
| ||
| 3 |
| 3 |
则CD=21+7
| 3 |
故答案是：21+7
| 3 |
点评：本题考查仰角的定义，要求学生能借助仰角构造直角三角形并解直角三角形．
练习册系列答案
口算题卡河北少年儿童出版社系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
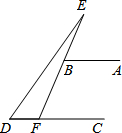（2013•荆州）如图，AB∥CD，∠ABE=60°，∠D=50°，则∠E的度数为（ ）
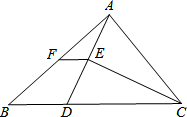（2013•荆州）如图，在△ABC中，BC＞AC，点D在BC上，且DC=AC，∠ACB的平分线CE交AD于E，点F是AB的中点，则S△AEF：S四边形BDEF为（ ）
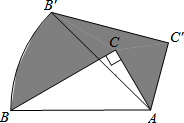（2013•荆州）如图，将含60°角的直角三角板ABC绕顶点A顺时针旋转45°度后得到△AB′C′，点B经过的路径为弧BB′，若∠BAC=60°，AC=1，则图中阴影部分的面积是（ ）
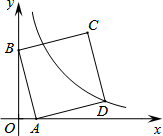（2013•荆州）如图，在平面直角坐标系中，直线y=-3x+3与x轴、y轴分别交于A、B两点，以AB为边在第一象限作正方形ABCD，点D在双曲线