��Ŀ����
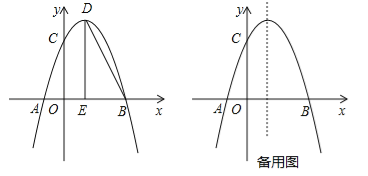
����Ŀ����ͼ1��ע����ͼ2��ȫ��ͬ�������κ���![]() ��ͼ����x�ύ��A��3��0����B����1��0�����㣬��y�ύ�ڵ�C��
��ͼ����x�ύ��A��3��0����B����1��0�����㣬��y�ύ�ڵ�C��
��1����ö��κ����Ľ���ʽ��
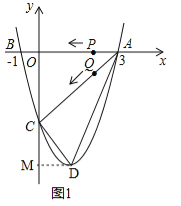
��2����������ߵĶ���ΪD������ACD�����������ͼ1��̽������
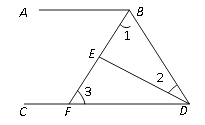
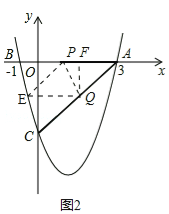
��3������P��Qͬʱ��A�����������ÿ��1����λ���ȵ��ٶȷֱ���AB��AC���˶�������һ�㵽��˵�ʱ����һ��Ҳ��ֹ֮ͣ�˶�����P��Q�˶���t��ʱ����APQ��PQ���ڵ�ֱ�߷��ۣ���Aǡ��������������E�㴦����ֱ���ж���ʱ�ı���APEQ����״�������E�����꣨����ͼ2��̽������

���𰸡���1��![]() ����2��4����3���ı���APEQΪ���Σ�E��
����2��4����3���ı���APEQΪ���Σ�E��![]() ��
��![]() ����
����
����������1�������κ���![]() ��ͼ����x�ύ��A��3��0����B����1��0������
��ͼ����x�ύ��A��3��0����B����1��0������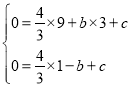 ����ã�
����ã�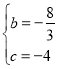 ����
����![]() ��
��
��2������D��DM��y���ڵ�M����![]() =
=![]() ������D��1��
������D��1��![]() ������C��0����4������S��ACD=S����AOMD��S��CDM��S��AOC=
������C��0����4������S��ACD=S����AOMD��S��CDM��S��AOC=![]() ����1+3����
����1+3����![]() ��
��![]() ����
����![]() ��4����1��
��4����1��![]() ��3��4=4��
��3��4=4��
��3���ı���APEQΪ���Σ�E������Ϊ��![]() ��
��![]() ��������������
��������������
��ͼ2��E�����PQ��A��Գƣ�����Q����QF��AP��F����AP=AQ=t��AP=EP��AQ=EQ����AP=AQ=QE=EP�����ı���AQEPΪ���Σ���FQ��OC����![]() ����
����![]() ����AF=
����AF=![]() t��FQ=
t��FQ=![]() t����Q��3��
t����Q��3��![]() t����
t����![]() t������EQ=AP=t����E��3��
t������EQ=AP=t����E��3��![]() t��t����
t��t����![]() t������E�ڶ��κ���
t������E�ڶ��κ���![]() �ϣ���
�ϣ���![]() ����t=
����t=![]() ����t=0����A�غϣ���ȥ������E��
����t=0����A�غϣ���ȥ������E��![]() ��
��![]() ����
����

 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д� ������ʱ����ҵ����ϵ�д�
������ʱ����ҵ����ϵ�д� ��ĩ���ƾ�ϵ�д�
��ĩ���ƾ�ϵ�д� ���ɿ��ñ���ϵ�д�
���ɿ��ñ���ϵ�д�