题目内容
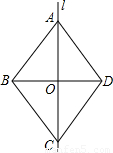
(2003•安徽)如图,l是四边形ABCD的对称轴,如果AD∥BC,有下列结论:①AB∥CD;②AB=BC;③AB⊥BC;④AO=OC,其中正确的结论是 (把你认为正确的结论的序号都填上).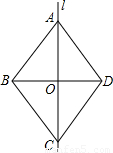
【答案】分析:根据轴对称的基本性质可知.
解答:解:因为l是四边形ABCD的对称轴,AD∥BC,
则AD=AB,∠DAC=∠BAC,∠DAC=∠BCA,
则∠BAC=∠BCA,
∴AB=BC,
∴AD=BC,
所以四边形ABCD是菱形.
所以①AB∥CD,正确;
②AB=BC,正确;
③AC⊥BD,错误;
④AO=OC,正确.
故正确的有①、②、④.
点评:此题考查轴对称的基本性质,注意:对称轴垂直平分对应点的连线,对应角相等,对应边相等.
解答:解:因为l是四边形ABCD的对称轴,AD∥BC,
则AD=AB,∠DAC=∠BAC,∠DAC=∠BCA,
则∠BAC=∠BCA,
∴AB=BC,
∴AD=BC,
所以四边形ABCD是菱形.
所以①AB∥CD,正确;
②AB=BC,正确;
③AC⊥BD,错误;
④AO=OC,正确.
故正确的有①、②、④.
点评:此题考查轴对称的基本性质,注意:对称轴垂直平分对应点的连线,对应角相等,对应边相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目