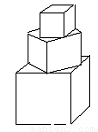
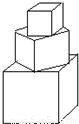
题目内容
有一塔形几何体由若干个正方体构成,构成方式如图所示:上层正方体底面的四个顶点恰好是下层正方体上底面各边的中点.已知最底层正方体的棱长为8,且该塔形几何体的全面积(含最底层正方体的底面面积)超过639,则该塔形中正方体的个数至少是 个.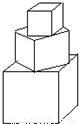
【答案】分析:设有n个正方体此正方体塔能看到表面及侧面和正方体裸露在外的上表面,根据题意知这n个正方体构成首相为8公比为 的等比序列.故这n个正方体的侧面又构成首相为64公比为
的等比序列.故这n个正方体的侧面又构成首相为64公比为 的等比序列.
的等比序列.
解答:解:设有n个正方体此正方体塔能看到表面及侧面和正方体裸露在外的上表面,则n个正方体侧面面积之和Sn= =16×(1+
=16×(1+ ),又知正方体裸露在上面的面积为64和最底层的面积64,故裸露在外面的表面积Sn'=64×(1+
),又知正方体裸露在上面的面积为64和最底层的面积64,故裸露在外面的表面积Sn'=64×(1+ )+64+64=64+26-n+64+64=198+26-n,由题意知Sn'>639.解之得n>10.
)+64+64=64+26-n+64+64=198+26-n,由题意知Sn'>639.解之得n>10.
故答案为10.
点评:本题需注意假如上面有一层立方体的话露出的表面积为:4×正方形的面积+一半正方形的面积,最底层的正方体露出的体积为:5×正方形的面积+一半正方形的面积.
 的等比序列.故这n个正方体的侧面又构成首相为64公比为
的等比序列.故这n个正方体的侧面又构成首相为64公比为 的等比序列.
的等比序列.解答:解:设有n个正方体此正方体塔能看到表面及侧面和正方体裸露在外的上表面,则n个正方体侧面面积之和Sn=
 =16×(1+
=16×(1+ ),又知正方体裸露在上面的面积为64和最底层的面积64,故裸露在外面的表面积Sn'=64×(1+
),又知正方体裸露在上面的面积为64和最底层的面积64,故裸露在外面的表面积Sn'=64×(1+ )+64+64=64+26-n+64+64=198+26-n,由题意知Sn'>639.解之得n>10.
)+64+64=64+26-n+64+64=198+26-n,由题意知Sn'>639.解之得n>10.故答案为10.
点评:本题需注意假如上面有一层立方体的话露出的表面积为:4×正方形的面积+一半正方形的面积,最底层的正方体露出的体积为:5×正方形的面积+一半正方形的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
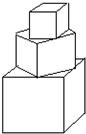 有一塔形几何体由若干个正方体构成,构成方式如图所示:上层正方体底面的四个顶点恰好是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形几何体的全面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是( )
有一塔形几何体由若干个正方体构成,构成方式如图所示:上层正方体底面的四个顶点恰好是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,且该塔形几何体的全面积(含最底层正方体的底面面积)超过39,则该塔形中正方体的个数至少是( ) 有一塔形几何体由若干个正方体构成,构成方式如图所示:上层正方体底面的四个顶点恰好是下层正方体上底面各边的中点.已知最底层正方体的棱长为8,且该塔形几何体的全面积(含最底层正方体的底面面积)超过639,则该塔形中正方体的个数至少是
有一塔形几何体由若干个正方体构成,构成方式如图所示:上层正方体底面的四个顶点恰好是下层正方体上底面各边的中点.已知最底层正方体的棱长为8,且该塔形几何体的全面积(含最底层正方体的底面面积)超过639,则该塔形中正方体的个数至少是