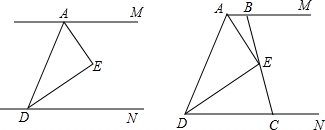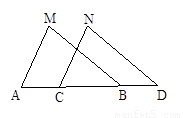题目内容
如图所示:AM∥DN,AE、DE分别平分∠MAD和∠AND,并交于E点.过点E的直线分别交AM、DN于B、C.
(1)如图,当点B、C分别位于点AD的同侧时,猜想AD、AB、CD之间的存在的数量关系:________.
(2)试证明你的猜想.
(3)若点B、C分别位于点AD的两侧时,试写出AD、AB、CD之间的关系,并选择一个写出证明过程.
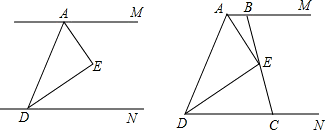
解: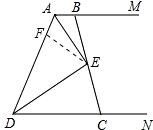 (1)AD=AB+CD;
(1)AD=AB+CD;
(2)证明:在AD上截取AF=AB,连接EF.
∵AE平分∠BAD,
∴∠BAE=∠FAE.
在△ABE和△AFE中,
AB=AF,∠BAE=∠FAE,AE=AE,
∴△ABE≌△AFE,
∴∠ABC=∠AFE.
∵AB∥CD,
∴∠ABC+∠BCD=180°,
又∵∠AFE+∠DFE=180°,
∴∠DFE=∠C.
∵DE平分∠ADC,
∴∠ADE=∠CDE.
在△FDE和△CDE中,
∠DFE=∠C,∠ADE=∠CDE,DE=DE,
∴△FDE≌△CDE,
∴DF=CD,
∴AF+DF=AB+CD.
即AD=AB+CD;
(3)证明:
第一种情况:当点B位于点A左侧,点C位于点D右侧时,DC=AD+AB.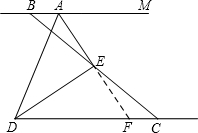
在CD上截取DF=AD,连接EF.
∵DE平分∠ADC
∴∠ADE=∠CDE
在△ADE和△FDE中,
DA=DF,∠ADE=∠CDE,DE=DE,
∴△ADE≌△FDE.
∴EA=EF,∠DAE=∠DFE.
∵AE平分∠DAM,
∴∠DAE=∠EAM,
∴∠DFE=∠EAM,
又∵∠BAE+∠EAM=180°,∠DFE+∠CFE=180°,
∴∠BAE=∠CFE.
∵AM∥DN,
∴∠ABC=∠BCD.
在△BAE和△CFE中,
∠BAE=∠CFE,∠ABC=∠BCD,EA=EF,
∴△BAE≌△CFE,
∴AB=FC.
∵DC=DF+FC,
∴DC=AD+AB;
第二种情况:当点B位于点A右侧,点C位于点D左侧时,AB=AD+CD.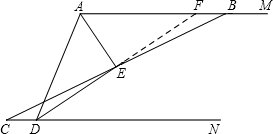
在AB上截取AF=AD,连接EF.
∵AE平分∠BAD,
∴∠BAE=∠DAE.
在△ADE和△AEF中,
AF=AD,∠BAE=∠DAE,AE=AE,
∴△AEF≌△AED,
∴EF=ED,
∴∠AFE=∠ADE.
∵DE平分∠ADN,
∴∠ADE=∠EDN,
∴∠AFE=∠EDN,
又∵∠AFE+∠BFE=180°,∠EDN+∠EDC=180°,
∴∠BFE=∠EDC.
∵AM∥DN,
∴∠ABC=∠BCD.
在△BEF和△CED中,
∠BFE=∠EDC,∠ABC=∠BCD,DE=EF,
∴△BFE≌△CDE,
∴CD=BF.
∵AB=AF+FB,
∴AB=AD+CD.
分析:(1)从图中可猜测AD=AB+CD.
(2)通过添加辅助线EF,构建全等三角形,根据全等三角形的性质判定△ABE≌△AFE,进而证明AD=AB+CD.
(3)当点B位于点A左侧,点C位于点D右侧时,DC=AD+AB;当点B位于点A右侧,点C位于点D左侧时,AB=AD+CD.
点评:本题主要考查全等三角形的性质与判定、角平分线的性质、平行线的性质,关键是添加好辅助线,构建好对应全等三角形,使问题得以解决.
 (1)AD=AB+CD;
(1)AD=AB+CD;(2)证明:在AD上截取AF=AB,连接EF.
∵AE平分∠BAD,
∴∠BAE=∠FAE.
在△ABE和△AFE中,
AB=AF,∠BAE=∠FAE,AE=AE,
∴△ABE≌△AFE,
∴∠ABC=∠AFE.
∵AB∥CD,
∴∠ABC+∠BCD=180°,
又∵∠AFE+∠DFE=180°,
∴∠DFE=∠C.
∵DE平分∠ADC,
∴∠ADE=∠CDE.
在△FDE和△CDE中,
∠DFE=∠C,∠ADE=∠CDE,DE=DE,
∴△FDE≌△CDE,
∴DF=CD,
∴AF+DF=AB+CD.
即AD=AB+CD;
(3)证明:
第一种情况:当点B位于点A左侧,点C位于点D右侧时,DC=AD+AB.

在CD上截取DF=AD,连接EF.
∵DE平分∠ADC
∴∠ADE=∠CDE
在△ADE和△FDE中,
DA=DF,∠ADE=∠CDE,DE=DE,
∴△ADE≌△FDE.
∴EA=EF,∠DAE=∠DFE.
∵AE平分∠DAM,
∴∠DAE=∠EAM,
∴∠DFE=∠EAM,
又∵∠BAE+∠EAM=180°,∠DFE+∠CFE=180°,
∴∠BAE=∠CFE.
∵AM∥DN,
∴∠ABC=∠BCD.
在△BAE和△CFE中,
∠BAE=∠CFE,∠ABC=∠BCD,EA=EF,
∴△BAE≌△CFE,
∴AB=FC.
∵DC=DF+FC,
∴DC=AD+AB;
第二种情况:当点B位于点A右侧,点C位于点D左侧时,AB=AD+CD.

在AB上截取AF=AD,连接EF.
∵AE平分∠BAD,
∴∠BAE=∠DAE.
在△ADE和△AEF中,
AF=AD,∠BAE=∠DAE,AE=AE,
∴△AEF≌△AED,
∴EF=ED,
∴∠AFE=∠ADE.
∵DE平分∠ADN,
∴∠ADE=∠EDN,
∴∠AFE=∠EDN,
又∵∠AFE+∠BFE=180°,∠EDN+∠EDC=180°,
∴∠BFE=∠EDC.
∵AM∥DN,
∴∠ABC=∠BCD.
在△BEF和△CED中,
∠BFE=∠EDC,∠ABC=∠BCD,DE=EF,
∴△BFE≌△CDE,
∴CD=BF.
∵AB=AF+FB,
∴AB=AD+CD.
分析:(1)从图中可猜测AD=AB+CD.
(2)通过添加辅助线EF,构建全等三角形,根据全等三角形的性质判定△ABE≌△AFE,进而证明AD=AB+CD.
(3)当点B位于点A左侧,点C位于点D右侧时,DC=AD+AB;当点B位于点A右侧,点C位于点D左侧时,AB=AD+CD.
点评:本题主要考查全等三角形的性质与判定、角平分线的性质、平行线的性质,关键是添加好辅助线,构建好对应全等三角形,使问题得以解决.

练习册系列答案
相关题目
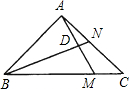 如图所示,在△ABC中,AM与BN相交于D,BM=3MC,AD=DM,求BD:DN的值.
如图所示,在△ABC中,AM与BN相交于D,BM=3MC,AD=DM,求BD:DN的值.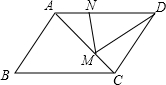 如图所示,在平行四边形ABCD中,M、N分别在AC、AD上,且AM=2CM,DN=2AN,若△DMN的面积为4,则平行四边形ABCD的面积为( )
如图所示,在平行四边形ABCD中,M、N分别在AC、AD上,且AM=2CM,DN=2AN,若△DMN的面积为4,则平行四边形ABCD的面积为( )