题目内容
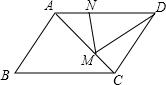 如图所示,在平行四边形ABCD中,M、N分别在AC、AD上,且AM=2CM,DN=2AN,若△DMN的面积为4,则平行四边形ABCD的面积为( )
如图所示,在平行四边形ABCD中,M、N分别在AC、AD上,且AM=2CM,DN=2AN,若△DMN的面积为4,则平行四边形ABCD的面积为( )分析:设平行四边形ABCD的面积为S,根据的高的三角形的面积的比等于底边的比表示出△AMD的面积,再表示出△DMN的面积,计算即可得解.
解答:解:设平行四边形ABCD的面积为S,
则S△ACD=
S,
∵AM=2CM,
∴S△AMD=
S△ACD=
S,
∵DN=2AN,
∴S△DMN=
S△AMD=
S,
∵△DMN的面积为4,
∴
S=4,
解得S=18.
故选B.
则S△ACD=
| 1 |
| 2 |
∵AM=2CM,
∴S△AMD=
| 2 |
| 1+2 |
| 1 |
| 3 |
∵DN=2AN,
∴S△DMN=
| 2 |
| 1+2 |
| 2 |
| 9 |
∵△DMN的面积为4,
∴
| 2 |
| 9 |
解得S=18.
故选B.
点评:本题考查了平行四边形的性质,主要利用了等高的三角形的面积的比等于底边的比,一定要熟练掌握并灵活运用.

练习册系列答案
相关题目
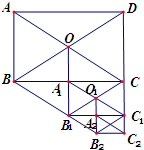 如图所示,在矩形ABCD中AB=12,AC=20,两条对角线相交于点O.以OB、OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1;再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1,O1C1为邻边作第3个平行四边形O1B1B2C1;…以此类推.
如图所示,在矩形ABCD中AB=12,AC=20,两条对角线相交于点O.以OB、OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1;再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1,O1C1为邻边作第3个平行四边形O1B1B2C1;…以此类推.

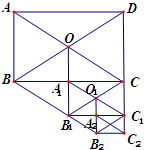 如图所示,在矩形ABCD中AB=12,AC=20,两条对角线相交于点O.以OB、OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1;再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1,O1C1为邻边作第3个平行四边形O1B1B2C1;…以此类推.
如图所示,在矩形ABCD中AB=12,AC=20,两条对角线相交于点O.以OB、OC为邻边作第1个平行四边形OBB1C,对角线相交于点A1;再以A1B1、A1C为邻边作第2个平行四边形A1B1C1C,对角线相交于点O1;再以O1B1,O1C1为邻边作第3个平行四边形O1B1B2C1;…以此类推.