Question

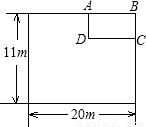
某单位为响应政府发出的全民健身的号召，打算在长和宽分别为20m和11m的矩形大厅内修建一个60m²的矩形健身房ABCD．该健身房的四面墙壁中有两侧沿用大厅的旧墙壁（如图为平面示意图），已知装修旧墙壁的费用为20元/m²，新建（含装修）墙壁的费用为80元/m²．设健身房的高为3m，一面旧墙壁AB的长为xm，修建健身房墙壁的总投入为y元．
（1）求y与x的函数关系式；
（2）为了合理利用大厅，要求自变量x必须满足条件：8≤x≤12，当投入的资金为4800元时，问利用旧墙壁的总长度为多少？

Answer 1

分析：（1）根据题意可得AB=x，AB•BC=60，所以BC=

60

x

．求得y与x的函数解析式．
（2）把y=4800代入函数解析式整理解得x的值即可．

解答：解：（1）根据题意，AB=x，AB•BC=60，
所以BC=

60

x

．
y=20×3（x+

60

x

）+80×3（x+

60

x

），
即y=300（x+

60

x

）．

（2）把y=4800代入y=300（x+

60

x

），得
4800=300（x+

60

x

）．
整理得x²-16x+60=0．
解得x₁=6，x₂=10．
经检验，x₁=6，x₂=10都是原方程的根．
由8≤x≤12，只取x=10．
所以利用旧墙壁的总长度10+

60

10

=16m．

点评：本题考查的是二次函数的实际应用同时也考查了矩形的面积计算公式．