题目内容
若关于x的方程(k2-2k)x2-(6k-4)x+8=0的解都是整数,试求实数k的值.分析:(1)根据k2-2k=0得出k的值,进而求出x的值;
(2)当k2-2k≠0进行分析,利用代入消元法求出k的值.
(2)当k2-2k≠0进行分析,利用代入消元法求出k的值.
解答:解:(1)当k2-2k=0,即k=0或k=2,
①若k=0时,原方程化为4x+8=0,即x=-2符合题意;
②若k=2时,原方程化为
-8x+8=0,
则x=1符合题意;
(2)当k2-2k≠0,即k≠0且k≠2时,原方程可化为:
(k2-2k)x2-(6k-4)x+8=0,
解得x1=
,x2=
,将k=
,代入x2=
得x1x2+2x1-x2-2=-2,
∴
或
或
或
∴
或
或
或
(舍去),
或
或
,
解得:k=1或-2或
,
综上:k的值为1,-2,
①若k=0时,原方程化为4x+8=0,即x=-2符合题意;
②若k=2时,原方程化为
-8x+8=0,
则x=1符合题意;
(2)当k2-2k≠0,即k≠0且k≠2时,原方程可化为:
(k2-2k)x2-(6k-4)x+8=0,
解得x1=
| 2 |
| k |
| 4 |
| k-2 |
| 2 |
| x1 |
| 4 |
| k-2 |
∴
|
|
|
|
∴
|
|
|
|
|
|
|
解得:k=1或-2或
| 2 |
| 3 |
综上:k的值为1,-2,
| 2 |
| 3 |
点评:此题主要考查了一元二次方程整数根的求法和代入消元法解方程,题目难度不大.

练习册系列答案
相关题目
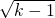 x+5=0是一元二次方程,求k的取值范围.
x+5=0是一元二次方程,求k的取值范围.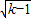 x+5=0是一元二次方程,求k的取值范围.
x+5=0是一元二次方程,求k的取值范围.