题目内容
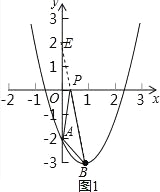
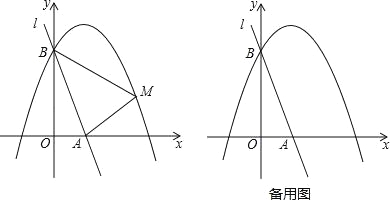
【题目】已知抛物线y=a（x﹣1）2﹣3（a≠0）的图象与y轴交于点A（0，﹣2），顶点为B．
（1）试确定a的值，并写出B点的坐标；
（2）若一次函数的图象经过A、B两点，试写出一次函数的解析式；
（3）试在x轴上求一点P，使得△PAB的周长取最小值；
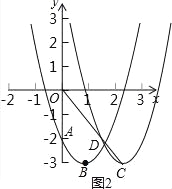
（4）若将抛物线平移m（m≠0）个单位，所得新抛物线的顶点记作C，与原抛物线的交点记作D，问：点O、C、D能否在同一条直线上？若能，请求出m的值；若不能，请说明理由．
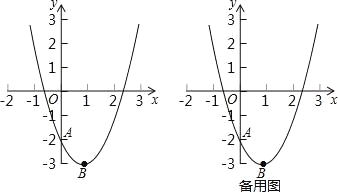
【答案】（1）a=1，B（1，-3）；（2）y=-x-2；（3）P（，0）；（4）能，m=2或-3.
【解析】
试题分析：（1）把A点坐标代入解析式中可求得a值，根据顶点式可写出B点坐标；（2）由（1）可知A、B坐标，直线AB解析式可求出；（3）找出A点关于x轴对称点E，连接BE交x轴于点P.求出BE解析式即可求出点P坐标；（4）如图2，设抛物线向右平移m（若m＞0表示向右平移，若m＜0表示向左平移）个单位，得到新的抛物线的顶点C（1+m，﹣3），可求出直线OC解析式，解新旧抛物线联立方程组求得交点D坐标为（
，
），把D坐标代到OC解析式中得到m=2或m=﹣3，即可得到结论．
试题解析： （1）把A（0，﹣2）代入y=a（x﹣1）2﹣3得﹣2=a（0﹣1）2﹣3，解得：a=1，∴y=（x﹣1）2﹣3，∴B（1，﹣3）；（2）设一次函数的解析式为y=kx+b，将A、B两点的坐标代入得：
，
解得
，∴一次函数的解析式为y=﹣x﹣2；（3）A点关于x轴的对称点记作E，则E（0，2），
如图1，连接EB交x轴于点P，则P点即为所求，设直线BE的解析式为y=px+q，则
，解得
，∴直线BE：y=﹣5x+2，当y=0时，0=-5x+2，解得x=-.∴P（，0）；（4）如图2，设抛物线向右平移m（若m＞0表示向右平移，若m＜0表示向左平移）个单位，则所得新的抛物线的顶点C（1+m，﹣3），∴直线OC的解析式为
，∴新抛物线解析式为 y=（x﹣1﹣m）2﹣3，解
，得
，∴两抛物线的交点D（， ），代入直线OC解析式中得
，解得：m=2或m=﹣3，∴O、C、D三点能够在同一直线上，
此时m=2或m=﹣3．
