题目内容
【题目】如图,A为∠MON内部一定点,点P、Q分别为射线OM,ON上的动点,若△APQ的周长最小时,∠PAQ=40°,则∠MON=_____.

【答案】70°
【解析】
作A关于ON的对称点E,A关于OM的对称点F,连接EF交OM于P,ON于Q,此时△APQ的周长最小=EF,由轴对称的性质和等腰三角形的性质即可得到结论.
作A关于ON的对称点E,A关于OM的对称点F,连接EF交OM于P,ON于Q,
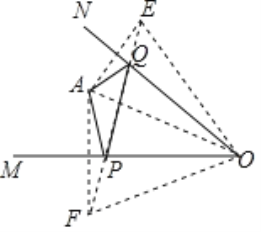
此时△APQ的周长最小=EF,
由轴对称的性质得到OE=OA=OF,∠EOQ=∠AOQ,∠FOP=∠AOP,
∴∠OEQ=∠OAQ,∠OFP=∠OAP,
∴∠OEF+∠OFE=∠OAQ+∠OAP=∠PAQ=40°,
∴∠EOF=180°﹣40°=140°,
∴∠MON=![]() ∠EOF=70°.
∠EOF=70°.
故答案为:70°.

练习册系列答案
相关题目









