题目内容
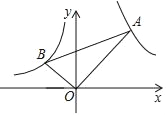
【题目】如图,在平面直角坐标系xOy中,点A的坐标是(0,2),点C是x轴上的一个动点.当点C在x轴上移动时,始终保持△ACP是等边三角形(点A、C、P按逆时针方向排列);当点C移动到点O时,得到等边三角形AOB(此时点P与点B重合)


初步探究
(1)写出点B的坐标 ;
(2)点C在x轴上移动过程中,当等边三角形ACP的顶点P在第三象限时,连接BP,求证:△AOC≌△ABP.
深入探究
(3)当点C在x轴上移动时,点P也随之运动.探究点P在怎样的图形上运动,请直接写出结论;
拓展应用
(4)点C在x轴上移动过程中,当△POB为等腰三角形时,直接写出此时点C的坐标.
【答案】(1)(![]() ,1);(2)证明见解析;(3)点P在过点B且垂直于AB的直线上; (4)点C的坐标为:(2,0)或(-
,1);(2)证明见解析;(3)点P在过点B且垂直于AB的直线上; (4)点C的坐标为:(2,0)或(-![]() ,0)或(-2,0)或C(-2
,0)或(-2,0)或C(-2![]() ,0).
,0).
【解析】
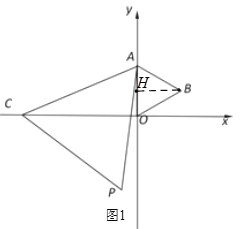
(1)如图1中,作BH⊥OA于H,利用等边三角形的性质,解直角三角形求出BH、OH即可得答案;
(2)由等边三角形的性质可得AO=AB,AC=AP,∠CAP=∠OAB=60°,继而可得∠CAO=∠PAB,利用SAS即可得证;
(3)由△AOC≌△ABP,可得∠ABP=∠AOC=90°,继而可得 点P在过点B且垂直于AB的直线上;
(4)分4种情况,①点C在x轴正半轴上,点P在第一象限时,BP=OB;②点C在x轴负半轴,点P在x轴正半轴时,OP=BP;③点C在x轴负半轴,点P在第四象限时,BP=OB;④点C在x轴负半轴,点P在y轴负半轴,针对四种情况分别画出图形并求解即可得.
(1)如图1中,作BH ⊥OA于H,
∵A(0,2),
∴OA=2,
∵△AOB是等边三角形,
∴OA=OB=AB=2,∠BOH=60°,
在Rt△OBH中,OH=AH=1,BH=![]() =
=![]() ,
,
∴B(![]() ,1);
,1);
(2)如图2,
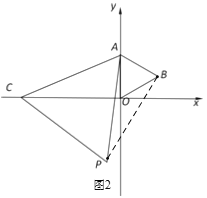
∵△AOB与△ACP都是等边三角形,
∴AO=AB,AC=AP,∠CAP=∠OAB=60°,
∴∠CAP+∠PAO=∠OAB+∠PAO,
即∠CAO=∠PAB,
∴△AOC≌△ABP(SAS);
(3)如图2中,∵△AOC≌△ABP,
∴∠ABP=∠AOC=90°,
∴PB⊥AB,
∴点P在过点B且垂直于AB的直线上;
(4)①如图3,当点C在x轴正半轴上,点P在第一象限时,BP=OB=2,

∵∠ABP=90°,
∴AP=![]() =2
=2![]() ,
,
∴AC=AP=2![]() ,
,
∴OC=![]() ,
,
∴C(2,0);
②如图4,当点C在x轴负半轴,点P在x轴正半轴时,OP=BP,此时AP垂直平分OB,
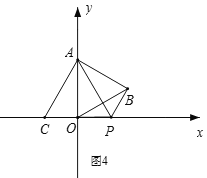
∴∠OAP=30°,
∴AP=PC=2OP,
∵AO2+OP2=AP2,即22+OP2=4OP2,
∴OP=![]() ,
,
∴OC=![]() ,
,
∴C(-![]() ,0);
,0);
③如图5,当点C在x轴负半轴,点P在第四象限时,BP=OB=2,
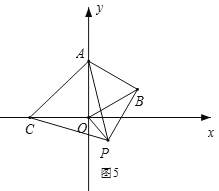
∵∠ABP=90°,
∴AP=![]() =2
=2![]() ,
,
∴AC=AP=2![]() ,
,
∴OC=![]() ,
,
∴C(-2,0);
④如图6,当点C在x轴负半轴,点P在y轴负半轴时,OP=OB=2,
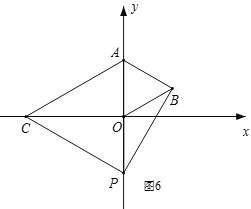
此时AP=2OP=4,∴AC=AP=4,
∵∠AOC=90°,OA=2,
∴OC=![]() ,
,
∴C(-2![]() ,0);
,0);
综上,点C的坐标为:(2,0)或(-![]() ,0)或(-2,0)或C(-2
,0)或(-2,0)或C(-2![]() ,0).
,0).

 备战中考寒假系列答案
备战中考寒假系列答案【题目】某商店购进一种商品,每件商品进价30元.试销中发现这种商品每天的销售量y(件)
与每件销售价x(元)的关系数据如下:
x | 30 | 32 | 34 | 36 |
y | 40 | 36 | 32 | 28 |
(1)已知y与x满足一次函数关系,根据上表,求出y与x之间的关系式(不写出自变量x的取值范围);
(2)如果商店销售这种商品,每天要获得150元利润,那么每件商品的销售价应定为多少元?
(3)设该商店每天销售这种商品所获利润为w(元),求出w与x之间的关系式,并求出每件商品销售价定为多少元时利润最大?