Question

【题目】试确定实数a的取值范围，使不等式组 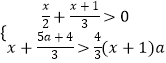恰有两个整数解．

Answer 1

【答案】解：由 ＞0，两边同乘以6得3x+2（x+1）＞0，解得x＞﹣ ， 由x+ ＞ （x+1）+a，两边同乘以3得3x+5a+4＞4（x+1）+3a，解得x＜2a，
∴原不等式组的解集为﹣ ＜x＜2a．
又∵原不等式组恰有2个整数解，即x=0，1；
则2a的值在1（不含1）到2（含2）之间，
∴1＜2a≤2，
∴0.5＜a≤1
【解析】先求出不等式组的解集，再根据x的两个整数解求出a的取值范围即可．
【考点精析】本题主要考查了一元一次不等式组的整数解的相关知识点，需要掌握使不等式组中的每个不等式都成立的未知数的值叫不等式组的解，一个不等式组的所有的解组成的集合，叫这个不等式组的解集(简称不等式组的解)才能正确解答此题．