题目内容
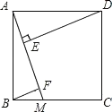
【题目】如图,正方形 ABCD 的边长为 5,点 M 是边 BC 上的点,DE⊥AM 于点 E,BF∥DE,交 AM 于点 F.若E 是 AF 的中点,则 DE 的长为( )
A.![]() B.2
B.2![]() C.4D.
C.4D.![]()
【答案】B
【解析】
因为AF=AE+EF,则可以通过证明![]() ABF≌
ABF≌![]() DAE,从而得到AE=BF,便得到了AF=BF+EF,再利用勾股定理求出DE的长即可.
DAE,从而得到AE=BF,便得到了AF=BF+EF,再利用勾股定理求出DE的长即可.
解:∵四边形ABCD是正方形,
∴AD=AB,∠BAD=90°
∵DE⊥AG,
∴∠DEM=∠AED=90°
∴∠ADE+∠DAE=90°
又∵∠BAF+∠DAE=∠BAD=90°,
∴∠ADE=∠BAF.
∵BF∥DE,
∴∠AFB=∠DEG=∠AED.
在![]() ABF与
ABF与![]() DAE中,
DAE中,
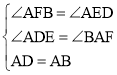 ,
,
∴![]() ABF≌
ABF≌![]() DAE(AAS).
DAE(AAS).
∴BF=AE,
∵BF∥DE,∠AED=90°
∴∠AFB=90°,
∵E是AF的中点,
∴AE=EF,
又∵BF=AE,
∴BF=EF=AE,
设BF为x,则AF为2x,
∵AB2=AF2+BF2,
∴52=(2x)2+x2,
解得x=![]() (舍去
(舍去![]() ),
),
∴AF=2x=![]() ,
,
∵DE=AF,
∴DE=![]() ,
,
故选:B.

练习册系列答案
相关题目