题目内容
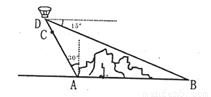
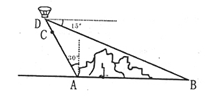
如图,在小山的西侧A处有一热气球,以30米/分钟的速度沿着与垂直方向所成夹角为30°的方向升空,40分钟后到达C处,这时热气球上的人发现,在A处的正东方向有一处着火点B,十分钟后,在D处测得着火点B的俯角为15°,求热气球升空点A与着火点B的距离。(结果保留根号,参考数据:
( ,
,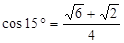 ,
, ,
,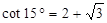 )。
)。
【答案】
1500(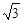 +1)米
+1)米
【解析】解:由题意可知,AD=(40+10)×30=1500(米)···1分
过点D作DH⊥BA,交BA延长线于点H。·········2分
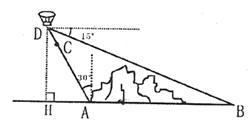
在Rt△DAH中,DH=AD·sin60°
=1500×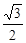 =750
=750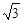 (米)。····4分
(米)。····4分
AH=AD·cos60°=1500×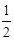 =750(米)。·······6分
=750(米)。·······6分
在Rt△DBH中,
BH=DH·cot15°=750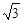 ×(2+
×(2+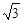 )=(1500
)=(1500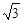 +2250)(米)···8分
+2250)(米)···8分
∴BA=BH-AH=1500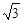 +2250-750=1500(
+2250-750=1500(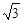 +1)(米)………..9分
+1)(米)………..9分
答:热气球升空点A与着火点B的距离为1500(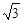 +1)(米)……10分
+1)(米)……10分
首先分析图形:根据题意构造直角三角形;本题涉及到两个直角三角形,应利用其公共边构造等量关系,进而可求出答案.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
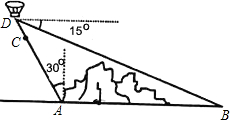 升空点A与着火点B的距离.(结果保留根号,参考数据:sin15°=
升空点A与着火点B的距离.(结果保留根号,参考数据:sin15°=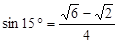 ,
,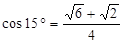 ,
, ,
,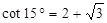 )。
)。
 升空点A与着火点B的距离.(结果保留根号,参考数据:sin15°=
升空点A与着火点B的距离.(结果保留根号,参考数据:sin15°= ,cos15°=
,cos15°=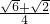 ,tan15°=2-
,tan15°=2- ,cot15°=2+
,cot15°=2+ ,cos15°=
,cos15°=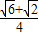 ,tan15°=2-
,tan15°=2-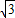 ,cot15°=2+
,cot15°=2+ )
)