题目内容
【题目】如图1,在ABCD中,AE⊥BC于E,E恰为BC的中点.tanB=2.
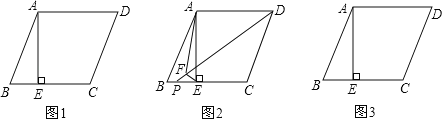
(1)求证:AD=AE;
(2)如图2.点P在BE上,作EF⊥DP于点F,连结AF.线段DF、EF与AF之间有怎样的数量关系?并说明理由;
(3)请你在图3中画图探究:当P为射线EC,上任意一点(P不与点E重合)时,作EF⊥DP于点F,连结AF,线段DF、EF与AF之间有怎样的数量关系?请在图3中补全图形,直接写出结论.
【答案】(1)见解析;(2)DF﹣EF=![]() AF,见解析;(3)①当EP在线段BC上时,有DF﹣EF=
AF,见解析;(3)①当EP在线段BC上时,有DF﹣EF=![]() AF,②当点F在PD上,DF+EF=
AF,②当点F在PD上,DF+EF=![]() AF,③当点F在PD的延长线上,EF﹣DF=
AF,③当点F在PD的延长线上,EF﹣DF=![]() AF,见解析.
AF,见解析.
【解析】
(1)首先根据∠B的正切值知:AE=2BE,而E是BC的中点,结合平行四边形的对边相等即可得证.
(2)此题要通过构造全等三角形来求解;作GA⊥AF,交BD于G,通过证△AFE≌△AGD,来得到△AFG是等腰直角三角形且EF=GD,由此得证.
(3)辅助线作法和解法同(2),只不过结论有所不同而已.
(1)证明:如图1中,
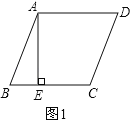
∵tanB=2,
∴AE=2BE;
∵E是BC中点,
∴BC=2BE,
即AE=BC;
又∵四边形ABCD是平行四边形,则AD=BC=AE;
(2)证明:作AG⊥AF,交DP于G;(如图2)
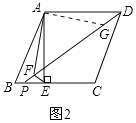
∵AD∥BC,
∴∠ADG=∠DPC;
∵∠AEP=∠EFP=90°,
∴∠PEF+∠EPF=∠PEF+∠AEF=90°,
即∠ADG=∠AEF=∠FPE;
又∵AE=AD,∠FAE=∠GAD=90°﹣∠EAG,
∴△AFE≌△AGD,
∴AF=AG,即△AFG是等腰直角三角形,且EF=DG;
∴FG=![]() AF,且DF=DG+GF=EF+FG,
AF,且DF=DG+GF=EF+FG,
故DF﹣EF=![]() AF;
AF;
(3)解:如图3,
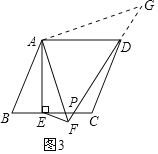
①当EP在线段BC上时,有DF﹣EF=![]() AF,
AF,
证明方法类似(2).
②如图3﹣1中,点F在PD上,DF+EF=![]() AF.
AF.
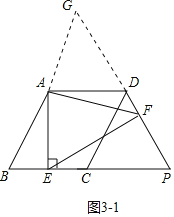
理由:将△AEF绕点A逆时针旋转90°得到△ADG
∴△AEF≌△ADG,
同(1)可得:DG=EF,AG=AF,
GF=![]() AF,
AF,
则EF+DF=![]() AF.
AF.
③如图3﹣2,点F在PD的延长线上,EF﹣DF=![]() AF,
AF,
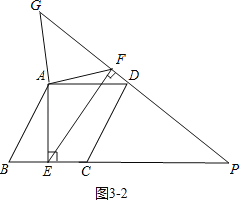
证明方法类似(2).

【题目】小王是“新星厂”的一名工人,请你阅读下列信息:
信息一:工人工作时间:每天上午8:00—12:00,下午14:00—18:00,每月工作25天;
信息二:小王生产甲、乙两种产品的件数与所用时间的关系见下表:
生产甲种产品数(件) | 生产乙种产品数(件) | 所用时间(分钟) |
10 | 10 | 350 |
30 | 20 | 850 |
信息三:按件计酬,每生产一件甲种产品得1.50元,每生产一件乙种产品得2.80元;
信息四:该厂工人每月收入由底薪和计酬工资两部分构成,小王每月的底薪为1900元.请根据以上信息,解答下列问题:
(1)小王每生产一件甲种产品和一件乙种产品分别需要多少分钟;
(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件,则小王该月收入最多是多少元?此时小王生产的甲、乙两种产品分别是多少件?