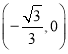Question

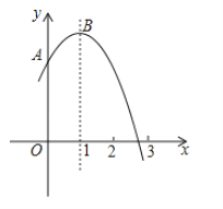
【题目】如图，抛物线为常数)交轴于点，与轴的一个交点在和之间，顶点为．

①抛物线与直线有且只有一个交点；

②若点、点、点在该函数图象上，则

③将该抛物线向左平移个单位，再向下平移个单位，所得抛物线解析式为；

④点关于直线的对称点为点分别在轴和轴上，当时，四边形周长的最小值为．

其中正确判断的序号是（ ）

A.①②③B.①②④C.②③④D.①③④

Answer 1

【答案】D

【解析】

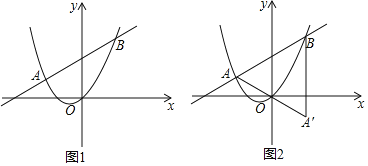
根据一元二次方程的判别式的值，即可判断①；根据抛物线的对称性和二次函数的增减性，即可判断②；根据二次函数的平移规律“左加右减，上加下减”即可判断③；先求出A，B，C的坐标，作点关于轴的对称点，作点关于轴的对称点连接，与轴、轴分别交于点，则四边形的最小周长，即可判断④．

把代入中，得，

，

一元二次方程两个相等的实数根，

∴抛物线与直线有且只有一个交点，

故此小题结论正确；

抛物线的对称轴为：直线，

点关于直线的对称点为，

，

当时，随增大而增大，

又，点、点、点在该函数图象上，

，

故此小题结论错误；

将该抛物线向左平移个单位，再向下平移个单位后，抛物线的解析式为：，即：，

故此小题结论正确；

当时，抛物线的解析式为：，

，

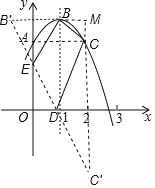
作点关于轴的对称点，作点关于轴的对称点连接，与轴、轴分别交于点，则，

根据两点之间线段最短，可知最短，而的长度一定，

四边形的最小周长

=

=

=．

故此小题结论正确；

综上所述：结论正确有，

故选D．