题目内容
、对于任意两个实数对(a,b)和(c,d),规定:当且仅当a=c且b=d时,(a,b)=(c,d).定义运算“ ”:(a,b)
”:(a,b) (c,d)=(ac-bd,ad+bc).若(1,2)
(c,d)=(ac-bd,ad+bc).若(1,2) (p,q)=(5,0),则p= ,q= .
(p,q)=(5,0),则p= ,q= .
 ”:(a,b)
”:(a,b) (c,d)=(ac-bd,ad+bc).若(1,2)
(c,d)=(ac-bd,ad+bc).若(1,2) (p,q)=(5,0),则p= ,q= .
(p,q)=(5,0),则p= ,q= .1,–2;
首先根据运算“⊕”:(a,b)⊕(c,d)=(ac-bd,ad+bc),可知(1,2)⊕(p,q)=(p-2q,q+2p),再由规定:当且仅当a=c且b=d时,(a,b)=(c,d),得出p-2q=5,q+2p=0,解关于p、q的二元一次方程组,即可得出结果.
解:根据题意可知(1,2)⊕(p,q)=(p-2q,q+2p)=(5,0),
∴p-2q=5,q+2p=0,
解得p=1,q=-2.
答案:1,-2.
点评:此题是定义新运算题型.直接把对应的数字代入所给的式子可求出所要的结果.
解题关键是对号入座不要找错对应关系.
解:根据题意可知(1,2)⊕(p,q)=(p-2q,q+2p)=(5,0),
∴p-2q=5,q+2p=0,
解得p=1,q=-2.
答案:1,-2.
点评:此题是定义新运算题型.直接把对应的数字代入所给的式子可求出所要的结果.
解题关键是对号入座不要找错对应关系.

练习册系列答案
相关题目
 ,B=
,B= ,求(3A-2B)-(2A+B)的值。
,求(3A-2B)-(2A+B)的值。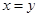 ,那么下列各式中正确的是( )
,那么下列各式中正确的是( )



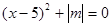 , (2)
, (2)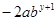 与
与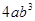 是同类项.求代数式:
是同类项.求代数式: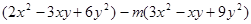 的值.
的值. 其中
其中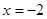 ,
,
 ( )
( )