��Ŀ����
����Ŀ����ƽ��ֱ������ϵ�У���A��1��0������֪������y=x2+mx��2m��m�dz�����������ΪP��
��1���������߾�����Aʱ��
����P�����ꣻ
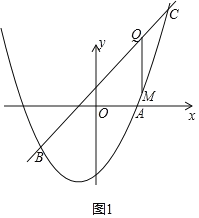
����ֱ��l��y=3x+1�������߽���B��C���㣬�������ϵĵ�M�ĺ�����Ϊn����1��n��3��������M��x��Ĵ��ߣ���ֱ��l���ڵ�Q����MQ=d����d��n�����������ʱ����n��ȡֵ��Χ��
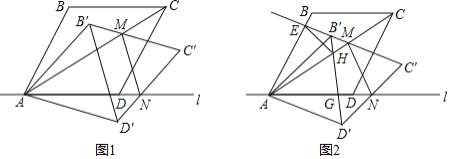
��2������mȡ��ֵ���������߶���������H������AHP=45��ʱ���������ߵĽ���ʽ��
���𰸡���1������P����![]() ����
����![]() ������1��n��3����2�������ߵı���ʽΪ��y=x2��4x+8��
������1��n��3����2�������ߵı���ʽΪ��y=x2��4x+8��![]() ��y=x2+4x��8��
��y=x2+4x��8��![]() ��
��
��������
��1���ٽ���A��������������߱���ʽ�ɵ�mֵ���ٸ��������߱���ʽȷ������P�����꼴�ɣ�
�ڻ�������ͼ��������������ֱ�߱���ʽ�ɵõ�B��C���꣬��֪��M�ĺ�����Ϊn����1��n��3��ʱ��ͼ���Ӧ����BC֮��IJ��֣����M��n��n2+n��2������Q��n��3n+1�����ɵ�d��n�Ĺ�ϵʽ����֪��Գ���Ϊn=1������d�������Կ�ȷ��n��ȡֵ��Χ��
��2����P������������![]() m����
m����![]() m2��2m�����ɵ�A��H������֪��AH=
m2��2m�����ɵ�A��H������֪��AH=![]() ��tan��=4����P������AH��������������������P��AH�Ҳ�ʱ������M��MR��AH�ڵ�R����RM=4x=RH����AR=x������AH=AR+RH�ɵ�xֵ����֪��M���꣬�ɵ�H��M����ɵ�ֱ��HM����ʽ������P������뼴�����mֵ���ڵ���P��AH���ʱ��ͬ�������M���꼰ֱ��HM�ı���ʽ������P������뼴�����mֵ.
��tan��=4����P������AH��������������������P��AH�Ҳ�ʱ������M��MR��AH�ڵ�R����RM=4x=RH����AR=x������AH=AR+RH�ɵ�xֵ����֪��M���꣬�ɵ�H��M����ɵ�ֱ��HM����ʽ������P������뼴�����mֵ���ڵ���P��AH���ʱ��ͬ�������M���꼰ֱ��HM�ı���ʽ������P������뼴�����mֵ.
�⣺��1���ٽ���A��1��0������y=x2+mx��2m��![]() ��
��
���![]()
���������ߵı���ʽΪy=x2+x��2��
![]()
![]() ��P����
��P����![]() ����
����![]() ����
����
�ں���ͼ����ͼ1��ʾ��
������������ֱ�߱���ʽ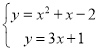
�ã�![]()
���x=��1��3��
��x=��1ʱ��![]() ��
��
��![]() ʱ��
ʱ�� ![]()
���Ե�B��C������ֱ�Ϊ������1����2������3��10����
��M�ĺ�����Ϊn����1��n��3��ʱ��ͼ���Ӧ����BC֮��IJ��֣�
���M��n��n2+n��2������Q��n��3n+1����
d=QM=3n+1��n2��n+2=��n2+2n+3�������ĶԳ���Ϊ��n=1��
��d��n����������٣�n��1������1��n��3��
��1��n��3��
��2����P������������![]() m����
m����![]() m2��2m����
m2��2m����
�ɵ�A��H������֪��AH=![]() ��tan��=4����P������AH����������������ͼ2��ʾ��
��tan��=4����P������AH����������������ͼ2��ʾ��
������P��AH�Ҳ�ʱ����ͼ��
����M��MR��AH�ڵ�R����AHP=45�㣬tan��=4��
�裺RM=4x=RH����AR=x��
��AH=AR+RH=5x=![]() ����ã�x=
����ã�x=![]() ��
��
��AM=![]() x=
x=![]() �����M��
�����M��![]() ��0����
��0����
��H��M�������ֱ��HM�ı���ʽΪ��y=��![]() x+
x+![]() ��
��
����P�����������ʽ�������ã�3m2+34m+88=0����ã�m=��4��![]() ��
��
�ڵ���P��AH���ʱ����ͼ��

ͬ���ɵã���M��5��0����
��ֱ��HM�ı���ʽΪ��y=![]() x+
x+![]() ��
��
����P�����������ʽ�������ã�7m2+48m+80=0��
��ã�m=4��![]() ��
��
���ϣ������ߵı���ʽΪ��y=x2��4x+8��y=x2��![]() x+
x+![]() ��y=x2+4x��8��y=x2+
��y=x2+4x��8��y=x2+![]() x��
x��![]() ��
��

����Ŀ����㻭ͼ��̽��δ֪����ͼ��仯���ɵ�һ����Ҫ����.������ͨ����㻭ͼ��֪����y��![]() ͼ��ı仯���ɵĹ���.
ͼ��ı仯���ɵĹ���.
��1���±���y��x�ļ����Ӧֵ������ɱ���.
x | ��1 | �� | 0 | 1 | 2 | 3 | 4 | �� |
y | 0 | 1 |
|
|
| �� |
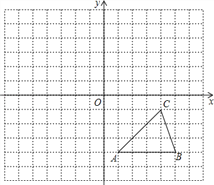
��2�������ϱ��е����ݣ���ƽ��ֱ������ϵxOy�������Ӧ�ĵ㣬����ƽ�����������ú�����ͼ��
��3������ͼ��д�������ú��������е����ʣ�
���ʢ� �� ����
���ʢ��� ����
��4����ֱ��y��x��ú�����ͼ��Ľ���A�ĺ�����Ϊa��ֱ�ӱȽ�a��![]() �Ĵ�С.
�Ĵ�С.

����Ŀ��ij����������������������ͳ�ƣ���������һ������ƽ��ÿ�������ʱ����ڵ��������������������в�������ͳ��ͼ����
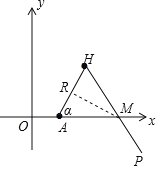
�����������ͳ��ͼ
�������ͳ�Ʊ�
����ʱ��� | �������������� |
| 16 |
|
|
| 37 |
| 12 |
| 30 |
�ϼ� |
|
����������Ϣ���ش��������⣺
��1��ƽ��ÿ�����������![]() ________��
________��![]() ʱ���ÿ�����������
ʱ���ÿ�����������![]() ___________��
___________��
��2�����![]() ʱ����������ε�Բ�ĽǵĶ�����
ʱ����������ε�Բ�ĽǵĶ�����
��3���������һ���������32000�����������![]() ʱ���ȫ���������ٱ���
ʱ���ȫ���������ٱ���
��4�������������ٳɱ���ͬʱ��֤������������ijʱ��αյ꣬�������һ���������Ľ��飮
����Ŀ��ij����������Ϊ���ܸ��õ��˽�ij���ȴ��綯�����������������ַ����β��ظ��ĸ���ȡ��10̨���綯��������������̵IJ��ԣ��������Ե�������������������ͷ��������������x��ʾ�����ֳ����飺��A��100��x��200����B��200��x��300����C��300��x��400����D��x��400����λ��km������������˲�����Ϣ��
��һ�γ�ȡ10̨�������������C���е������ǣ�380��310��300��310��
�ڶ��γ�ȡ10̨������������ǣ�220��301��175��310��400��310��385��430��234��455��
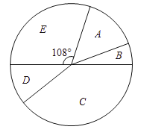
��һ�β��Ե������������ͳ��ͼ��ͼ
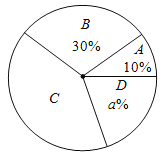
���β��Ե��������ͳ�Ʊ�
��һ�� | �ڶ��� | |
ƽ����� | 321.4 | b |
��� | c | 310 |
���� | 310 | 310 |
����������Ϣ������������⣺
��1��ֱ��д������ͼ����a��b��c��ֵ��a���� ����b���� ����c�� ����
��2�������������ݣ�����Ϊ�����β����е���һ�εĴ��綯��������������ǿ����˵�����ɣ�һ�����ɼ��ɣ���
��3������������һ���ȹ�����1600̨���綯��������������β��ԣ�������һ��������������ǿ��x��380���Ĵ��綯�����ж�������