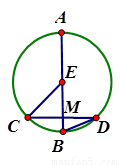
题目内容
如图,CD是⊙E的弦,直径AB过CD的中点M,若∠BEC=40°,则∠ABD=
- A.40°
- B.60°
- C.70°
- D.80°
C
试题分析: 为弧
为弧 所对的圆心角与圆周角,根据圆周角定理可求∠BDC,由垂径定理可知AB⊥CD,在Rt△BDM中,由互余关系可求∠ABD.解:∵
所对的圆心角与圆周角,根据圆周角定理可求∠BDC,由垂径定理可知AB⊥CD,在Rt△BDM中,由互余关系可求∠ABD.解:∵ 为弧
为弧 所对的圆心角与圆周角∴∠BDC=20°,∵CD是⊙O的弦,直径AB过CD的中点M,∴AB⊥CD,∴在Rt△BDM中,∠ABD=90°-∠BDC=70°.故选C.
所对的圆心角与圆周角∴∠BDC=20°,∵CD是⊙O的弦,直径AB过CD的中点M,∴AB⊥CD,∴在Rt△BDM中,∠ABD=90°-∠BDC=70°.故选C.
考点:本题考查了垂径定理
点评:此类试题属于难度很大的试题,考生一定要把握好垂径定理和圆周角、圆心角等的基本关系和性质定理
试题分析:
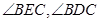 为弧
为弧 所对的圆心角与圆周角,根据圆周角定理可求∠BDC,由垂径定理可知AB⊥CD,在Rt△BDM中,由互余关系可求∠ABD.解:∵
所对的圆心角与圆周角,根据圆周角定理可求∠BDC,由垂径定理可知AB⊥CD,在Rt△BDM中,由互余关系可求∠ABD.解:∵ 为弧
为弧 所对的圆心角与圆周角∴∠BDC=20°,∵CD是⊙O的弦,直径AB过CD的中点M,∴AB⊥CD,∴在Rt△BDM中,∠ABD=90°-∠BDC=70°.故选C.
所对的圆心角与圆周角∴∠BDC=20°,∵CD是⊙O的弦,直径AB过CD的中点M,∴AB⊥CD,∴在Rt△BDM中,∠ABD=90°-∠BDC=70°.故选C.考点:本题考查了垂径定理
点评:此类试题属于难度很大的试题,考生一定要把握好垂径定理和圆周角、圆心角等的基本关系和性质定理

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
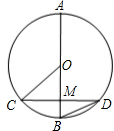 如图,CD是⊙O的弦,直径AB过CD的中点M,若∠BOC=40°,则∠ABD=( )
如图,CD是⊙O的弦,直径AB过CD的中点M,若∠BOC=40°,则∠ABD=( )| A、40° | B、60° | C、70° | D、80° |
 23、如图,CD是⊙O的弦,AB是直径,CD⊥AB,垂足为P,求证:PC2=PA•PB.
23、如图,CD是⊙O的弦,AB是直径,CD⊥AB,垂足为P,求证:PC2=PA•PB.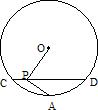 17、(按非课改要求命制)如图,CD是⊙O的弦,点P在弦CD上,点A是弧CD的中点,过点P作PA⊥OP交⊙O于点A,已知,CP=2cm,PD=8cm,则PA=
17、(按非课改要求命制)如图,CD是⊙O的弦,点P在弦CD上,点A是弧CD的中点,过点P作PA⊥OP交⊙O于点A,已知,CP=2cm,PD=8cm,则PA= 如图,CD是⊙O的弦,直径AB过CD的中点M,若∠BOC=40°,则∠ABD=
如图,CD是⊙O的弦,直径AB过CD的中点M,若∠BOC=40°,则∠ABD=