题目内容
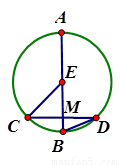
 如图,CD是⊙O的弦,直径AB过CD的中点M,若∠BOC=40°,则∠ABD=
如图,CD是⊙O的弦,直径AB过CD的中点M,若∠BOC=40°,则∠ABD=70°
70°
.分析:由CD是⊙O的弦,直径AB过CD的中点M,根据垂径定理即可得AB⊥CD,又由圆周角定理,可求得∠BDC的度数,继而求得答案.
解答:解:∵CD是⊙O的弦,直径AB过CD的中点M,
∴AB⊥CD,
∵∠BDC=
∠BOC=
×40°=20°,
∴∠ABD=90°-∠BDC=70°.
故答案为:70°.
∴AB⊥CD,
∵∠BDC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠ABD=90°-∠BDC=70°.
故答案为:70°.
点评:此题考查了圆周角定理与垂径定理.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
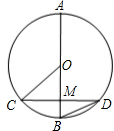 如图,CD是⊙O的弦,直径AB过CD的中点M,若∠BOC=40°,则∠ABD=( )
如图,CD是⊙O的弦,直径AB过CD的中点M,若∠BOC=40°,则∠ABD=( )| A、40° | B、60° | C、70° | D、80° |
 23、如图,CD是⊙O的弦,AB是直径,CD⊥AB,垂足为P,求证:PC2=PA•PB.
23、如图,CD是⊙O的弦,AB是直径,CD⊥AB,垂足为P,求证:PC2=PA•PB.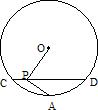 17、(按非课改要求命制)如图,CD是⊙O的弦,点P在弦CD上,点A是弧CD的中点,过点P作PA⊥OP交⊙O于点A,已知,CP=2cm,PD=8cm,则PA=
17、(按非课改要求命制)如图,CD是⊙O的弦,点P在弦CD上,点A是弧CD的中点,过点P作PA⊥OP交⊙O于点A,已知,CP=2cm,PD=8cm,则PA=