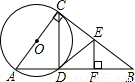
题目内容
已知:如图,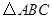 中,
中,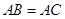 ,以
,以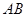 为直径的⊙O交
为直径的⊙O交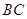 于点
于点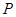 ,
,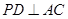 于点
于点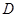 .
.
(1)求证: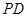 是⊙O的切线;
是⊙O的切线;
(2)若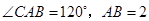 ,求
,求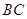 的值.
的值.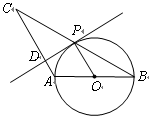
(1)见解析;(2)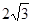
解析试题分析:(1)由OB=OP可得∠B=∠OPB,由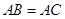 可得∠B=∠C,即可证得OP∥AC,再结合
可得∠B=∠C,即可证得OP∥AC,再结合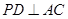 即可证得结论;
即可证得结论;
(2)连接AP,根据直径所对是圆周角是直角可得AP⊥BC,再根据等腰三角形的三线合一的性质可得BP=CP,最后利用含30°角的直角三角形的性质结合勾股定理即可求得结果。
(1)∵OB=OP
∴∠B=∠OPB
∵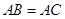
∴∠B=∠C
∴∠C=∠OPB
∴OP∥AC
∴∠OPD=∠CDP=90°
∵OP是半径
∴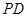 是⊙O的切线;
是⊙O的切线;
(2)连接AP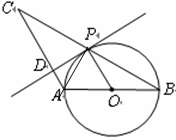
∵AB是直径
∴AP⊥BC
∵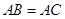
∴BP=CP,∠B=∠C
∵∠CAB=120°
∴∠B=∠C=30°
∴在Rt△ABP中,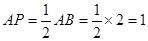
在Rt△ABP中,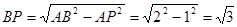
∴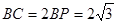 .
.
考点:本题考查的是切线的判定及性质,勾股定理
点评:解答本题的关键是熟记要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
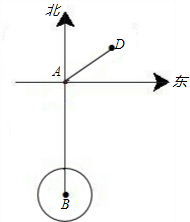 中新网2010年8月23日电.中央气象台消息,今日8时,南海热带低压加强为今年第5号热带风暴“蒲公英”,逐渐向海南岛南部近海靠近.已知,如图,一艘轮船以20海里/时的速度由西向东航行,在途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心
中新网2010年8月23日电.中央气象台消息,今日8时,南海热带低压加强为今年第5号热带风暴“蒲公英”,逐渐向海南岛南部近海靠近.已知,如图,一艘轮船以20海里/时的速度由西向东航行,在途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,距台风中心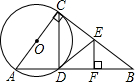 AB,垂足为F.
AB,垂足为F.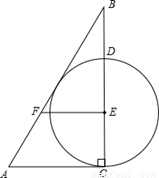
 BC;
BC;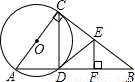
 BC;
BC;