题目内容
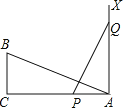
【题目】在Rt△ABC中, ∠C=90,sinB=
，点D在BC边上，且∠ADC=45，BD=2.
（1）求BC,AB的长；
（2）求∠BAD的正切值.
【答案】（1）BC=8，AB=10；（2）
【解析】
第一问根据正弦值解三角形，第二问利用第一问得到的三边边长根据余弦定理算出余弦，进而求出正切.
（1）因为∠C=90，sinB=
，所以tanB=
，即
，而由∠ADC=45得△ADC是等腰直角三角形，故AC=CD，结合BD=2解得AC=CD=6，故BC=BD+CD=8，AB=
=10，所以BC=8，AB=10；（2）由第一问可知AB=10，BD=2,AD=6
,在三角形ABD中利用余弦定理可得cos∠BAD=
=
=
，利用正弦余弦平方之和等于1可得sin∠BAD=
,显然∠BAD为锐角，sin∠BAD=
，tan∠BAD=
=.
练习册系列答案
相关题目
【题目】2018年3月，某市教育主管部门在初中生中开展了“文明礼仪知识竞赛”活动，活动结束后，随机抽取了部分同学的成绩（x均为整数，总分100分），绘制了如下尚不完整的统计图表．
调查结果统计表
组别 | 成绩分组（单位：分） | 频数 | 频率 |
A | 80≤x＜85 | 50 | 0.1 |
B | 85≤x＜90 | 75 | |
C | 90≤x＜95 | 150 | c |
D | 95≤x≤100 | a | |
合计 | b | 1 |
根据以上信息解答下列问题：
（1）统计表中，a= ，b= ，c= ；
（2）扇形统计图中，m的值为 ，“C”所对应的圆心角的度数是 ；
（3）若参加本次竞赛的同学共有5000人，请你估计成绩在95分及以上的学生大约有多少人？
