题目内容
(2013•黄石模拟)4月20日8时2分,四川省雅安市芦山县发生了7.0级地震,当地的部分房屋严重受损,上万灾民无家可归,灾情牵动亿万中国人的心.某市积极筹集救灾物质 260吨物资从该市区运往雅安甲、乙两地,若用大、小两种货车共20辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如下表:
(1)求这两种货车各用多少辆?
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);
(3)在(2)的条件下,若运往甲地的物资不少于132吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.
| 车 型 运往地 |
甲 地(元/辆) | 乙 地(元/辆) |
| 大货车 | 720 | 800 |
| 小货车 | 500 | 650 |
(2)如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);
(3)在(2)的条件下,若运往甲地的物资不少于132吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.
分析:(1)首先设大货车用x辆,则小货车用(20-x)辆,利用所运物资为260吨得出等式方程求出即可;
(2)根据安排9辆货车前往甲地,前往甲地的大货车为a辆,得出小货车的辆数,进而得出w与a的函数关系;
(3)根据运往甲地的物资不少于132吨,则16a+10(9-a)≥132即可得出a的取值范围,进而得出最佳方案.
(2)根据安排9辆货车前往甲地,前往甲地的大货车为a辆,得出小货车的辆数,进而得出w与a的函数关系;
(3)根据运往甲地的物资不少于132吨,则16a+10(9-a)≥132即可得出a的取值范围,进而得出最佳方案.
解答:解:(1)设大货车用x辆,则小货车用(20-x)辆,根据题意得
16x+10(20-x)=260,
解得:x=10,
∴20-x=10.
答:大货车用10辆,小货车用10辆.
(2)由题意得出:
w=720a+800(10-a)+500(9-a)+650[10-(9-a)]
=70a+13150,
∴w=70a+13150(0≤a≤10且为整数).
(3)由16a+10(9-a)≥132,
解得a≥7.
又∵0≤a≤10,∴7≤a≤10且为整数.
∵w=70a+13150,k=70>0,w随a的增大而增大,
∴当a=7时,w最小,最小值为W=70×7+13150=13640.
答:使总运费最少的调配方案是:7辆大货车、2辆小货车前往甲地;3辆大货车、
8辆小货车前往乙地.最少运费为13640元.
16x+10(20-x)=260,
解得:x=10,
∴20-x=10.
答:大货车用10辆,小货车用10辆.
(2)由题意得出:
w=720a+800(10-a)+500(9-a)+650[10-(9-a)]
=70a+13150,
∴w=70a+13150(0≤a≤10且为整数).
(3)由16a+10(9-a)≥132,
解得a≥7.
又∵0≤a≤10,∴7≤a≤10且为整数.
∵w=70a+13150,k=70>0,w随a的增大而增大,
∴当a=7时,w最小,最小值为W=70×7+13150=13640.
答:使总运费最少的调配方案是:7辆大货车、2辆小货车前往甲地;3辆大货车、
8辆小货车前往乙地.最少运费为13640元.
点评:此题主要考查了一次函数的应用以及一元一次不等式的应用和最佳方案问题,此题综合性较强,难度较大,应注意最佳方案的选择.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
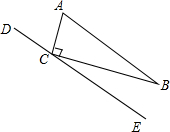 (2013•黄石模拟)如图,Rt△ABC中,∠ACB=90°,DE经过点C且平行于AB,∠A=65°,则∠BCE的度数是( )
(2013•黄石模拟)如图,Rt△ABC中,∠ACB=90°,DE经过点C且平行于AB,∠A=65°,则∠BCE的度数是( )