题目内容
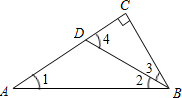
如图，△ABC中，∠C=90°，∠ABC=60°，BD平分∠ABC，若AD=6，求AC的长．
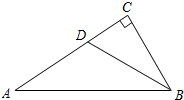
∵△ABC中，∠C=90°，∠ABC=60°，BD平分∠ABC，
∴∠2=∠3=30°；
在Rt△BCD中，
CD=
BD，∠4=90°-30°=60°（直角三角形的两个锐角互余）；
∴∠1+∠2=60°（外角定理），
∴∠1=∠2=30°，
∴AD=BD（等角对等边）；
∴AC=AD+CD=
AD；
又∵AD=6，
∴AC=9．
∴∠2=∠3=30°；
在Rt△BCD中，
CD=
| 1 |
| 2 |
∴∠1+∠2=60°（外角定理），
∴∠1=∠2=30°，
∴AD=BD（等角对等边）；
∴AC=AD+CD=
| 3 |
| 2 |
又∵AD=6，
∴AC=9．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
相关题目
