题目内容
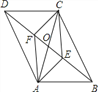
【题目】在四边形ABCD中，AD∥BC，点E在BC边的延长线上，CE=BC，连接AE，交CD边于点F，且CF=DF． 
（1）如图1，求证：AD=BC；
（2）如图2，连接BD、DE，若BD⊥DE，请判定四边形ABCD的形状，并证明．
【答案】
（1）证明：∵AD∥BC，
∴∠D=∠ECF，
在△ADF和△ECF中，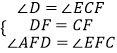 
，
∴△ADF≌△ECF（ASA），
∴AD=CE，
∵CE=BC，
∴AD=BC
（2）解：四边形ABCD是菱形；理由如下：
∵AD∥BC，AD=BC，
∴四边形ABCD是平行四边形，
∵BD⊥DE，
∴∠BDE=90°，
∵CE=BC，
∴CD= 
BE=BC，
∴四边形ABCD是菱形
【解析】（1）由平行线的性质得出∠D=∠ECF，由ASA证明△ADF≌△ECF，得出AD=CE，即可得出结论；（2）首先四边形ABCD是平行四边形，由直角三角形斜边上的中线性质得出CD= BE=BC，即可得出四边形ABCD是菱形．
【考点精析】利用平行线的性质对题目进行判断即可得到答案，需要熟知两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补．
名校课堂系列答案
【题目】在某市2016年“书香校园，经典诵读”比赛活动中，有32万名学生参加比赛活动，其中有8万名学生分别获得一、二、三等奖，从获奖学生中随机抽取部分，绘制成不完整的统计表（如表），请根据图表解答下列问题．
获奖等级 | 频数 |
一等奖 | a |
二等奖 | b |
三等奖 | 275 |
（1）表格中a的值为 ， b的值为 ．
（2）扇形统计图中表示获得一等奖的扇形的圆心角为度．
（3）估计全市有多少名学生获得三等奖？
【题目】某市甲、乙两个汽车销售公司，去年一至十月份每月销售同种品牌汽车的情况如图所示：
（1）请你根据左图填写右表：
销售公司 | 平均数 | 方差 | 中位数 | 众数 |
甲 | 9 | |||
乙 | 9 | 17.0 | 8 |
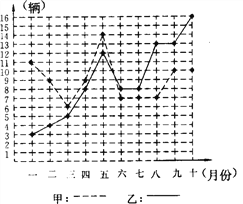
（2）请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析：
①从平均数和方差结合看；
②从折线图上甲、乙两个汽车销售公司销售数量的趋势
看（分析哪个汽车销售公司较有潜力）．
