题目内容
已知,A(3,a)是双曲线y=| 12 |
| x |
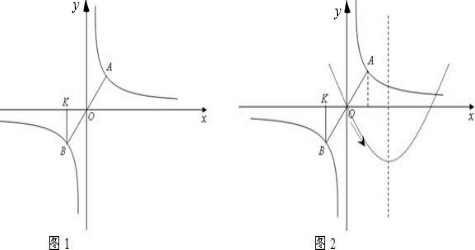
(1)试求a的值与点B坐标;
(2)在直角坐标系中,先使线段AB在x轴的正方向上平移6个单位,得线段A1B1,再依次在与y轴平行的方向上进行第二次平移,得线段A2B2,且可知两次平移中线段AB先后滑过的面积相等(即?AA1B1B与?A1A2B2B1的面积相等).求出满足条件的点A2的坐标,并说明△AA1A2与△OBK是否相似的理由;
(3)设线段AB中点为M,又如果使线段AB与双曲线一起移动,且AB在平移时,M点始终在抛物线y=
| 1 |
| 6 |
(4)试探究:在(3)基础上,如果线段AB按如图2所示方向滑过的面积为24个平方单位,且M点始终在直线x=6的左侧,试求此时线段AB所在直线与x轴交点的坐标,以及M点的横坐标.
分析:(1)将A点坐标代入反比例函数的解析式中,即可求得a的值,而A、B关于原点对称,由此求出B点的坐标.
(2)根据A、B的坐标知:A、B的横向、纵向距离分别为6、8,若线段AB向x轴正方向移动6个单位,那么它的面积应该是6×8=48,由于?AA1B1B与?A1A2B2B1的面积相等,而A、B的横距离为6,那么第二次平移的距离必为8个单位,然后分向上、向下平移两种情况分类讨论即可得到点A2的坐标;
在求△AA1A2与△OBK是否相似,已知∠OKB=∠AA1A2=90°,只需比较两组直角边是否对应成比例即可.
(3)已知了M、A的横、纵坐标的差分别为3、4,因此将过M的抛物线向右平移3个单位后,再向上平移4个单位,即可得到所求的抛物线解析式.
(4)易知AB=10,若平移后扫过的面积为24,那么线段AB平行移动的距离为
,过A作x轴的垂线,设垂足为T,则T到AB的距离为
,也就是说点T在平移后的直线AB上(即平移后的直线AB与x轴的交点),易求得直线AB的斜率,结合点T的坐标,即可得到平移后直线AB的解析式,联立抛物线的解析式可求得M点的横坐标.
(2)根据A、B的坐标知:A、B的横向、纵向距离分别为6、8,若线段AB向x轴正方向移动6个单位,那么它的面积应该是6×8=48,由于?AA1B1B与?A1A2B2B1的面积相等,而A、B的横距离为6,那么第二次平移的距离必为8个单位,然后分向上、向下平移两种情况分类讨论即可得到点A2的坐标;
在求△AA1A2与△OBK是否相似,已知∠OKB=∠AA1A2=90°,只需比较两组直角边是否对应成比例即可.
(3)已知了M、A的横、纵坐标的差分别为3、4,因此将过M的抛物线向右平移3个单位后,再向上平移4个单位,即可得到所求的抛物线解析式.
(4)易知AB=10,若平移后扫过的面积为24,那么线段AB平行移动的距离为
| 12 |
| 5 |
| 12 |
| 5 |
解答:解:(1)将A代入双曲线y=
中,可得a=
,
故a=4,A(3,4);
由于A、B关于原点对称,那么B(-3,-4).(2分)
(2)∵A(3,4),B(-3,-4),则AB间的横向距离、纵向距离分别为6、8个单位,
∴由题意可得:?AA1B1B的面积为48,
又∵?AA1B1B与?A1A2B2B1的面积相等,
∴第二次线段A1B1进一步在纵向平移了8个单位.
故:AA1=6,A1A2=8
可知,第二次在平移的方向上可能向上,也可能向下.
∴①当线段向上平移时:A(3,4)→A1(9,4)→A2(9,12);
②当线段向下平移时:A(3,4)→A1(9,4)→A2(9,-4).
所以A2的坐标为:(9,12)或(9,-4)(2分)
又∵OK=3,KB=4,
∴
=
=
,
而∠OKB=∠AA1A2=90°,
故:△AA1A2∽△OBK.(2分)
(3)由题意可知:将抛物线y=
(x-6)2-6向右平移3个单位,再向上平移4个单位,得:
A点满足的解析式为:y=
(x-9)2-2.(2分)
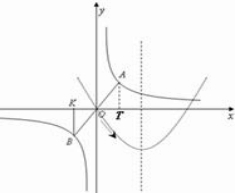 (4)∵AB=10且使线段AB按如图所示方向滑过的面积为24个平方单位,M在直线x=6的左侧,
(4)∵AB=10且使线段AB按如图所示方向滑过的面积为24个平方单位,M在直线x=6的左侧,
∴AB在平移前后的平行距离为
;
过A(3,4)点作AT⊥x轴于T,又可得T点到平移前线段AB的距离为
;
∴平移后AB直线与x轴的交点必为T(3,0).(2分)
又可知平移后AB直线解析式为:y=
x-4,此时M为抛物线:y=
(x-6)2-6与直线:y=
x-4的交点,
∴解方程:
(x-6)2-6=
x-4,
得:x=10±2
,
又∵0<x<6,
∴x=10-2
,
故M的横坐标为10-2
.(2分)
| 12 |
| x |
| 12 |
| 3 |
故a=4,A(3,4);
由于A、B关于原点对称,那么B(-3,-4).(2分)
(2)∵A(3,4),B(-3,-4),则AB间的横向距离、纵向距离分别为6、8个单位,
∴由题意可得:?AA1B1B的面积为48,
又∵?AA1B1B与?A1A2B2B1的面积相等,
∴第二次线段A1B1进一步在纵向平移了8个单位.
故:AA1=6,A1A2=8
可知,第二次在平移的方向上可能向上,也可能向下.
∴①当线段向上平移时:A(3,4)→A1(9,4)→A2(9,12);
②当线段向下平移时:A(3,4)→A1(9,4)→A2(9,-4).
所以A2的坐标为:(9,12)或(9,-4)(2分)
又∵OK=3,KB=4,
∴
| OK |
| AA1 |
| 1 |
| 2 |
| BK |
| A2A1 |
而∠OKB=∠AA1A2=90°,
故:△AA1A2∽△OBK.(2分)
(3)由题意可知:将抛物线y=
| 1 |
| 6 |
A点满足的解析式为:y=
| 1 |
| 6 |
 (4)∵AB=10且使线段AB按如图所示方向滑过的面积为24个平方单位,M在直线x=6的左侧,
(4)∵AB=10且使线段AB按如图所示方向滑过的面积为24个平方单位,M在直线x=6的左侧,∴AB在平移前后的平行距离为
| 12 |
| 5 |
过A(3,4)点作AT⊥x轴于T,又可得T点到平移前线段AB的距离为
| 12 |
| 5 |
∴平移后AB直线与x轴的交点必为T(3,0).(2分)
又可知平移后AB直线解析式为:y=
| 4 |
| 3 |
| 1 |
| 6 |
| 4 |
| 3 |
∴解方程:
| 1 |
| 6 |
| 4 |
| 3 |
得:x=10±2
| 19 |
又∵0<x<6,
∴x=10-2
| 19 |
故M的横坐标为10-2
| 19 |
点评:此题是反比例函数和二次函数的综合题,涉及到函数图象上点的坐标意义、图象的平移变换、图形面积的求法、函数图象的几何变换、函数图象交点坐标的求法等重要知识,难度较大.

练习册系列答案
相关题目
 如图,在直线L上依次摆放着三个正方形,已知中间斜放置的正方形的面积是6,则正放置的两个正方形的面积之和为( )
如图,在直线L上依次摆放着三个正方形,已知中间斜放置的正方形的面积是6,则正放置的两个正方形的面积之和为( )| A、6 | ||
| B、5 | ||
C、
| ||
| D、36 |
 15、如图,已知:平行四边形ABCD中,E是CD边的中点,连接BE并延长与AD的延长线相交于F点.求证:BC=DF.
15、如图,已知:平行四边形ABCD中,E是CD边的中点,连接BE并延长与AD的延长线相交于F点.求证:BC=DF. 19、某学校准备从甲、乙、丙、丁四位学生中选出一名学生做学生会干部,对四位学生进行了德、智、体、美、劳的综合测试,四人成绩如下表.同时又请100位同学对四位同学做推荐选举投票,投票结果如扇形统计图所示,学校决定综合测试成绩与民主推荐的分数比是6:4,即:综合测试成绩的60%和民主推荐成绩的40%计入总成绩.最后分数最高的当选为学生会干部.请你完成下列问题:
19、某学校准备从甲、乙、丙、丁四位学生中选出一名学生做学生会干部,对四位学生进行了德、智、体、美、劳的综合测试,四人成绩如下表.同时又请100位同学对四位同学做推荐选举投票,投票结果如扇形统计图所示,学校决定综合测试成绩与民主推荐的分数比是6:4,即:综合测试成绩的60%和民主推荐成绩的40%计入总成绩.最后分数最高的当选为学生会干部.请你完成下列问题: