Question

如图，在Rt△ABC中，∠C=90°，AC=6cm，BC=8cm点P、Q同时由A、B两点出发，分别沿AC、BC方向都以1cm/s的速度匀速移动，几秒后△PCQ的面积是△ABC面积的一半？

Answer 1

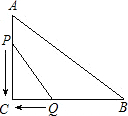
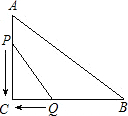
设t秒后△PCQ的面积是△ABC面积的一半，
则可得此时PC=AC-AP=6-t，CQ=BC-BQ=8-t，
∴△ABC面积为

1

2

×AC×BC=

1

2

×6×8=24，△PCQ的面积为

1

2

×PC×CQ=

1

2

×(6-t)×(8-t)，
∵△PCQ的面积是△ABC面积的一半，
∴

1

2

×(6-t)×(8-t)=

1

2

×24，
解得t₁=2，t₂=12（不合题意舍去），
即2秒后△PCQ的面积是△ABC面积的一半．
答：2秒后△PCQ的面积是△ABC面积的一半．