题目内容
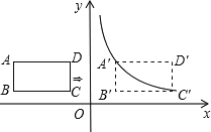
【题目】如图,OABC是一张放在平面直角坐标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,
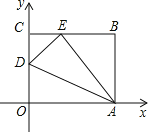
(1)求D、E两点的坐标.
(2)求过D、E两点的直线函数表达式
【答案】(1) D(0,5);E(4,8).(2)![]() .
.
【解析】
试题(1)先根据勾股定理求出BE的长,进而可得出CE的长,求出E点坐标,在Rt△DCE中,由DE=OD及勾股定理可求出OD的长,进而得出D点坐标.
(2)由(1)知D、E的坐标,根据待定系数法即可求得表达式.
试题解析:(1)依题意可知,折痕AD是四边形OAED的对称轴,
∴在Rt△ABE中,AE=AO=10,AB=8,BE=![]() =6,
=6,
∴CE=4,
∴E(4,8).
在Rt△DCE中,DC2+CE2=DE2,
又∵DE=OD,
∴(8-OD)2+42=OD2,
∴OD=5,
∴D(0,5),
综上D点坐标为(0,5)、E点坐标为(4,8).
(2)由(1)得: E(4,8).D(0,5),
设直线DE的解析式为y=mx+n,
∴![]() ,
,
解得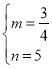 ,
,
∴直线DE的解析式为y=![]() x+5.
x+5.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
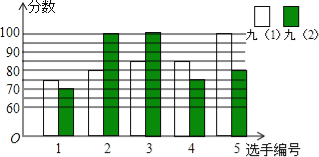
【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
(1)根据图示填写下表;
班级 | 平均数(分) | 中位数(分) | 众数(分) |
九(1) | 85 | 85 | |
九(2) | 80 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好;
(3)计算两班复赛成绩的方差.