题目内容
观察下列不等式:
32-12=8×1.52-32=8×2.72-52=8×3.92-72=8×4…
(1)用含有字母n(n≥1的整数)的等式表示这一规律;
(2)请用所学知识验证这个规律的正确性;
(3)借助你发现的规律把400写成两个正整数的平方差的形式:
400=( )2-( )2.
32-12=8×1.52-32=8×2.72-52=8×3.92-72=8×4…
(1)用含有字母n(n≥1的整数)的等式表示这一规律;
(2)请用所学知识验证这个规律的正确性;
(3)借助你发现的规律把400写成两个正整数的平方差的形式:
400=( )2-( )2.
分析:(1)观察一系列等式得到一般性规律,写出即可;
(2)利用平方差公式化简已知等式左边,得到结果与右边相同,得证;
(3)根据得出的规律即可得到结果.
(2)利用平方差公式化简已知等式左边,得到结果与右边相同,得证;
(3)根据得出的规律即可得到结果.
解答:解:(1)根据题意得:(2n+1)2-(2n-1)2=8n(n≥1的整数);
(2)左边=[(2n+1)+(2n-1)][(2n+1)-(2n-1)]=4n×2=8n=右边,
则(2n+1)2-(2n-1)2=8n(n≥1的整数);
(3)400=8×50=(2×50+1)2-(2×50-1)2=1012-992.
(2)左边=[(2n+1)+(2n-1)][(2n+1)-(2n-1)]=4n×2=8n=右边,
则(2n+1)2-(2n-1)2=8n(n≥1的整数);
(3)400=8×50=(2×50+1)2-(2×50-1)2=1012-992.
点评:此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.

练习册系列答案
相关题目
 )2+(
)2+( )2>2×
)2>2× 2>2×
2>2×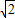 )2+(
)2+( )2>2×
)2>2×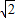 ×
×
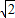 )2+
)2+ 2>2×
2>2× ×
×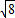 +
+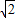 )2+(
)2+(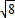 )2>2×
)2>2×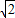 ×
× ,a2+b2> (a≠b).
,a2+b2> (a≠b).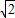 )2+(
)2+( )2>2×
)2>2×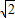 ×
×
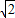 )2+
)2+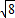 2>2×
2>2× ×
×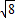 +
+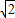 )2+(
)2+( )2>2×
)2>2×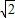 ×
×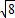 ,a2+b2> (a≠b).
,a2+b2> (a≠b).