题目内容
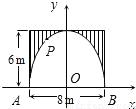
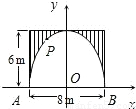
(2005•绵阳)有一个抛物线形的拱形隧道,隧道的最大高度为6m,跨度为8m,把它放在如图所示的平面直角坐标系中.(1)求这条抛物线所对应的函数关系式;
(2)若要在隧道壁上点P(如图)安装一盏照明灯,灯离地面高4.5m.求灯与点B的距离.
【答案】分析:(1)根据抛物线在坐标系的位置可设解析式:y=ax2+6,把点A(-4,0)代入即可;
(2)灯离地面高4.5m,即y=4.5时,求x的值,再根据P点坐标,勾股定理求PB的值
解答: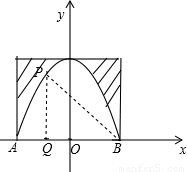 解:(1)由题意,设抛物线所对应的函数关系为y=ax2+6(a<9),
解:(1)由题意,设抛物线所对应的函数关系为y=ax2+6(a<9),
∵点A(-4,0)或B(4,0)在抛物线上,
∴0=a•(-4)2+6,
16a+6=0,
16a=-6,
a=- .
.
故抛物线的函数关系式为y=- x2+6.
x2+6.
(2)过点P作PQ⊥AB于Q,连接PB,则PQ=4.5m.
将y=4.5代入y=- x2+6中,
x2+6中,
4.5=- x2+6,
x2+6,
- x2=4.5-6,
x2=4.5-6,
x=±2.
∴P(-2,4.5),Q(-2,0),
于是|PQ|=4.5,|BQ|=6,
从而|PB|=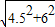 =
=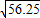 =7.5.
=7.5.
所以照明灯与点B的距离为7.5m.
点评:本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.
(2)灯离地面高4.5m,即y=4.5时,求x的值,再根据P点坐标,勾股定理求PB的值
解答:
 解:(1)由题意,设抛物线所对应的函数关系为y=ax2+6(a<9),
解:(1)由题意,设抛物线所对应的函数关系为y=ax2+6(a<9),∵点A(-4,0)或B(4,0)在抛物线上,
∴0=a•(-4)2+6,
16a+6=0,
16a=-6,
a=-
 .
.故抛物线的函数关系式为y=-
 x2+6.
x2+6.(2)过点P作PQ⊥AB于Q,连接PB,则PQ=4.5m.
将y=4.5代入y=-
 x2+6中,
x2+6中,4.5=-
 x2+6,
x2+6,-
 x2=4.5-6,
x2=4.5-6,x=±2.
∴P(-2,4.5),Q(-2,0),
于是|PQ|=4.5,|BQ|=6,
从而|PB|=
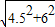 =
=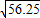 =7.5.
=7.5.所以照明灯与点B的距离为7.5m.
点评:本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ?若存在,指出其中的一种平移方式;若不存在,请说明理由;
?若存在,指出其中的一种平移方式;若不存在,请说明理由;
 ?若存在,指出其中的一种平移方式;若不存在,请说明理由;
?若存在,指出其中的一种平移方式;若不存在,请说明理由;