题目内容

因式分解及计算：
（1）分解因式：9（m+n）2-（m-n）2
（2）计算：（
x+3
x-3
-
x-3
x+3
）÷
12x
x2-6x+9
．
分析：（1）运用平方差公式分解因式；
（2）括号里通分，将除法转化为乘法，因式分解，约分．
解答：解：（1）9（m+n）2-（m-n）2
=[3（m+n）]2-（m-n）2
=[3（m+n）+（m-n）][3（m+n）-（m-n）]
=4（2m+n）（m+2n）；
（2）原式=
(x+3)2-(x-3)2
(x-3)(x+3)
•
(x-3)2
12x

=
12x
x+3
•
x-3
12x
=
x-3
x+3
．
点评：本题考查分式的混合运算，运用公式法因式分解．进行分式混合运算时，关键是通分，合并同类项，注意混合运算的运算顺序．
练习册系列答案
相关题目
28、问题1：同学们已经体会到灵活运用乘法公式给整式乘法及多项式的因式分解带来的方便，快捷．相信通过下面材料的学习探究，会使你大开眼界并获得成功的喜悦．
例：用简便方法计算195×205．
解：195×205
=（200-5）（200+5）           ①
=2002-52                   ②
=39975
（1）例题求解过程中，第②步变形是利用
平方差公式
（填乘法公式的名称）．
（2）用简便方法计算：9×11×101×10001（4分）
问题2：对于形如x2+2xa+a2这样的二次三项式，可以用公式法将它分解成（x+a）2的形式．但对于二次三项式x2+2xa-3a2，就不能直接运用公式了．
此时，我们可以在二次三项式x2+2xa-3a2中先加上一项a2，使它与x2+2xa的和成为一个完全平方式，再减去a2，整个式子的值不变，于是有：x2+2xa-3a2=（x2+2ax+a2）-a2-3a2=（x+a）2-4a2=（x+a）2-（2a）2=（x+3a）（x-a）
像这样，先添一适当项，使式中出现完全平方式，再减去这个项，使整个式子的值不变的方法称为“配方法”．
利用“配方法”分解因式：a2-6a+8．
31、问题1：同学们已经体会到灵活运用乘法公式给整式乘法及多项式的因式分解带来的方便，快捷．相信通过下面材料的学习、探究，会使你大开眼界，并获得成功的喜悦．
例：用简便方法计算195×205．
解：195×205
=（200-5）（200+5）①
=2002-52②
=39975
（1）例题求解过程中，第②步变形是利用
平方差公式
（填乘法公式的名称）；
（2）用简便方法计算：9×11×101×10001．
问题2：对于形如x2+2ax+a2这样的二次三项式，可以用公式法将它分解成（x+a）2的形式．但对于二次三项式x2+2ax-3a2，就不能直接运用公式了．此时，我们可以在二次三项式x2+2ax-3a2中先加上一项a2，使它与x2+2ax的和成为一个完全平方式，再减去a2，整个式子的值不变，于是有：
x2+2ax-3a2=（x2+2ax+a2）-a2-3a2
=（x+a）2-（2a）2
=（x+3a）（x-a）．
像这样，先添一适当项，使式中出现完全平方式，再减去这个项，使整个式子的值不变的方法称为“配方法”．
（1）利用“配方法”分解因式：a2-4a-12．
问题3：若x-y=5，xy=3，求：①x2+y2；②x4+y4的值．

问题1：同学们已经体会到灵活运用乘法公式给整式乘法及多项式的因式分解带来的方便，快捷.相信通过下面材料的学习探究，会使你大开眼界并获得成功的喜悦.例：用简便方法计算195×205.

解:195×205

=(200-5)(200+5)          ①

=2002-52                  ②

=39975

（1）例题求解过程中，第②步变形是利用             （填乘法公式的名称）

（2）用简便方法计算：9×11×101

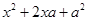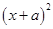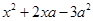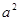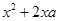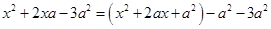
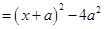
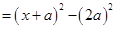
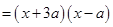
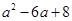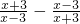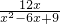问题2:对于形如这样的二次三项式，可以用公式法将它分解成的形式.但对于二次三项式，就不能直接运用公式了.此时，我们可以在二次三项式中先加上一项，使它与的和成为一个完全平方式，再减去，整个式子的值不变，于是有:

（3）像这样，先添一适当项，使式中出现完全平方式，再减去这个项，使整个式子的值不变的方法称为“配方法”.利用“配方法”分解因式:.

 

因式分解及计算：
（1）分解因式：9（m+n）2-（m-n）2
（2）计算：（数学公式）÷数学公式．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网