题目内容
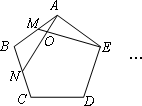
 如图,正五边形ABCD中,点F、G分别是BC、CD的中点,AF与BG相交于H.
如图,正五边形ABCD中,点F、G分别是BC、CD的中点,AF与BG相交于H.
(1)求证:△ABF≌△BCG;
(2)求∠AHG的度数.
(1)证明:∵五边形ABCDE是正五边形,
∴AB=BC=CD,∠ABC=∠BCD,(2分)
∴F、G分别是BC、CD的中点,
∴BF=CG,(4分)
在△ABF和BCG中,
AB=BC,∠ABC=∠BCD,BF=CG,(5分)
∴△ABF≌△BCG;(6分)
(2)解:由(1)知∠GBC=∠FAB,
∵∠AHG=∠FAB+∠ABH=∠GBC+∠ABH=∠ABC(,7分)
∵正五边形的内角为108°,
∴∠AHG=108°.(9分)
(注:本小题直接正确写出∠AHG=108°不扣分)
分析:(1)利用正五边形的相等的角和相等的边得到证明全等三角形的条件后证明全等即可;
(2)将∠AHG的度数转化为正五边形的内角的度数求解.
点评:本题考查了正多边形的计算及全等三角形的判定及性质,解题的关键是正确地利用正五边形中相等的元素.
∴AB=BC=CD,∠ABC=∠BCD,(2分)
∴F、G分别是BC、CD的中点,
∴BF=CG,(4分)
在△ABF和BCG中,
AB=BC,∠ABC=∠BCD,BF=CG,(5分)
∴△ABF≌△BCG;(6分)
(2)解:由(1)知∠GBC=∠FAB,
∵∠AHG=∠FAB+∠ABH=∠GBC+∠ABH=∠ABC(,7分)
∵正五边形的内角为108°,
∴∠AHG=108°.(9分)
(注:本小题直接正确写出∠AHG=108°不扣分)
分析:(1)利用正五边形的相等的角和相等的边得到证明全等三角形的条件后证明全等即可;
(2)将∠AHG的度数转化为正五边形的内角的度数求解.
点评:本题考查了正多边形的计算及全等三角形的判定及性质,解题的关键是正确地利用正五边形中相等的元素.

练习册系列答案
相关题目

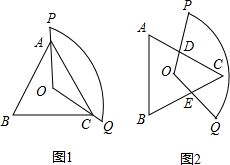
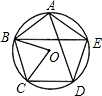 如图,若五边形ABCDE是⊙O的内接正五边形,则∠BOC=
如图,若五边形ABCDE是⊙O的内接正五边形,则∠BOC=